Физическая сторона задачи

Будем полагать, что материал линейно упруг и следует закону Гука. Обобщенный закон Гука запишется:

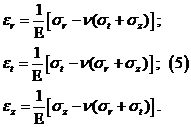
Из последнего уравнения имеем

Исключим из двух первых уравнений

аналогично: (5,а)

Уравнение равновесия (1) тождественно удовлетворяется, если ввести следующую функцию F:

На самом деле:

(тождество).

Выразим в (5а) деформации через функцию напряжений

б)

Подставим (7) и (5б) в уравнение совместимости деформаций (4)

Получаем следующее дифференциальное уравнение

Найдем решение этого уравнения. Будем искать его в форме , где - произвольная постоянная.

подставим в (8):

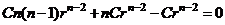. т.к. и , то сократив на и 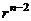, получаем

При каждом из значений 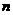имеем частное решение уравнения (8), а общее решение однородного уравнения (8) равняется сумме линейно-независимых частных решений

Зная функцию напряжений 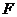, легко найти напряжения

Эти уравнения можно объединить в одну формулу:

Это и есть формулы Ляме для напряжений в толстостенном цилиндре. Постоянные интегрирования 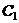и 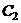определяются из граничных условий.