
Запишем граничные условия.
1) при 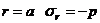
2) при 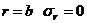
Подставим это в выражение для 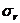 из формулы (10)
из формулы (10) 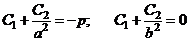
Решая полученную систему уравнений, определяем 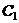 и
и 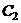
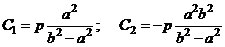 Подставим в (10)
Подставим в (10)
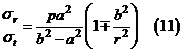
Напряжения распределяются по гиперболическому закону. Характер распределения напряжений показан на рисунке. Наибольшие окружные напряжения возникают в точках внутреннего контура.
Обратимся к осевым напряжениям
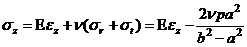
Оказывается осевое напряжение постоянно по сечению цилиндра.
Здесь возможны два различных случая:
а) Цилиндр имеет днище. В этом случае растягивающая цилиндр сила равна давлению на дно 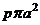 и осевые напряжения равны
и осевые напряжения равны
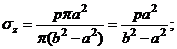
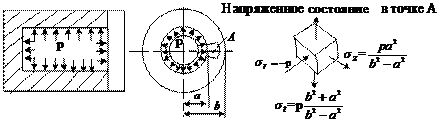 Наиболее опасной оказывается точка “A”, принадлежащая внутреннему контуру.
Наиболее опасной оказывается точка “A”, принадлежащая внутреннему контуру.
Главные напряжения в ней равны:
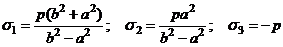
Если принять гипотезу наибольших касательных напряжений, то эквивалентное напряжение равно
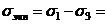
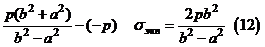
б) Цилиндр открыт (например, ствол орудия) 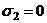
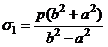 ;
; 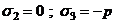
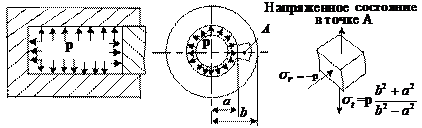 Т.к. эквивалентное напряжение от
Т.к. эквивалентное напряжение от 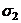 не зависит, то оно выражается той же самой формулой (12).
не зависит, то оно выражается той же самой формулой (12).
Цилиндр с бесконечно толстыми стенками.
Если 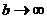 , то из (11) следует
, то из (11) следует 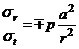 ,
,
т.е. радиальное напряжение по модулю равно окружному.
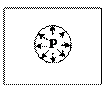
Практически этим результатом можно пользоваться при 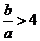 . Интересно, что при этом форма внешнего контура не играет никакой роли.
. Интересно, что при этом форма внешнего контура не играет никакой роли.
Эквивалентное напряжение в этом случае 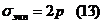
 2018-01-21
2018-01-21 549
549








