Теорема про існування та єдиність розв’язку задачі Коші диференціального рівняння першого порядку, що розв’язане відносно похідної

Теорема (про існування та єдиність розв’язку задачі Коші). Нехай у диференціальному рівнянні функція визначена в прямокутнику

і задовольняє умовам:

1) неперервна по та у ;

2) задовольняє умові Ліпшиця по змінній , тобто

Тоді існує єдиний розв’язок диференціального рівняння, який визначений при , і задовольняє умові , де

Доведення. Розглянемо простір, елементами якого є функції , неперервні на відрізку й обмежені . Введемо метрику . Одержимо повний метричний простір . Замінимо диференціальне рівняння , еквівалентним інтегральним рівнянням

Розглянемо оператор Через те, що ,

то оператор ставить у відповідність кожній неперервній функції , визначеній при й обмежений також неперервну функцію , визначену при й обмежену . Перевіримо, чи є оператор оператором стиску.

І оскільки , то оператор є оператором стиску , . Відповідно до принципу стислих відображень операторне рівняння має єдиний розв’язок, тобто інтегральне рівняння 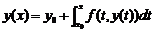, чи задача Коші для диференціального рівняння , також має єдиний розв’язок.

Зауваження. Умову Ліпшиця можна замінити іншою, більш грубою, але легше перевіряємою умовою існування обмеженої по модулю частинної похідної в області . Дійсно,