Розглянемо лінійні однорідні диференціальні рівняння з сталими коефіцієнтами 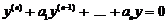 .
.
Розв’язок будемо шукати у вигляді 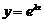 . Продиференціювавши, одержимо
. Продиференціювавши, одержимо 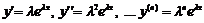 . Підставивши
. Підставивши 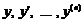 в диференціальне рівняння, отримаємо
в диференціальне рівняння, отримаємо 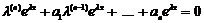 . Скоротивши на
. Скоротивши на 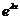 , одержимо характеристичне рівняння
, одержимо характеристичне рівняння 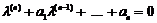 . Алгебраїчне рівняння
. Алгебраїчне рівняння 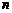 -го степеня має
-го степеня має 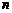 - коренів. У залежності від їхнього вигляду будемо мати різні розв’язки.
- коренів. У залежності від їхнього вигляду будемо мати різні розв’язки.
1) Нехай 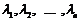 - дійсні і різні. Тоді функції
- дійсні і різні. Тоді функції 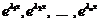 є розв’язками й оскільки всі
є розв’язками й оскільки всі 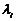 різні, то
різні, то 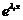 - розв’язки лінійно незалежні, тобто
- розв’язки лінійно незалежні, тобто 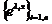 фундаментальна система розв’язків. Загальним розв’язком буде лінійна комбінація
фундаментальна система розв’язків. Загальним розв’язком буде лінійна комбінація 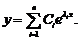
2) Нехай маємо комплексно спряжені корені 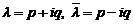 . Їм відповідають розв’язки
. Їм відповідають розв’язки 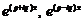 . Розкладаючи їх по формулі Ейлера, одержимо:
. Розкладаючи їх по формулі Ейлера, одержимо:
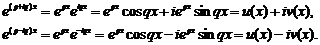
І, як випливає з властивості 4, функції 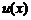 й
й 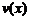 будуть окремими розв’язками. Таким чином, кореням
будуть окремими розв’язками. Таким чином, кореням 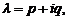
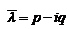 відповідають два лінійно незалежних розв’язки
відповідають два лінійно незалежних розв’язки 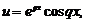
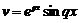 . Загальним розв’язком, що відповідає цим двом кореням, буде
. Загальним розв’язком, що відповідає цим двом кореням, буде 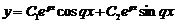 .
.
3) Нехай 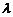 - кратний корінь, кратності
- кратний корінь, кратності 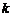 , тобто
, тобто 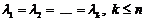 .
.
a) Розглянемо випадок 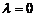 . Тоді характеристичне рівняння
. Тоді характеристичне рівняння 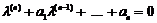
вироджується в рівняння 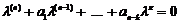 .
.
Диференціальне рівняння, що відповідає цьому характеристичному, запишеться у вигляді 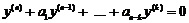 . Неважко бачити, що частковими, лінійно незалежними розв’язками цього рівняння, будуть функції
. Неважко бачити, що частковими, лінійно незалежними розв’язками цього рівняння, будуть функції 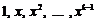 . Загальним розв’язком, що відповідає кореню
. Загальним розв’язком, що відповідає кореню 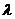 кратності
кратності 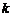 , буде лінійна комбінація цих функцій
, буде лінійна комбінація цих функцій 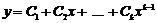 .
.
б) Нехай 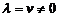 - корінь дійсний. Зробивши заміну
- корінь дійсний. Зробивши заміну 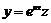 , на підставі властивості 2 лінійних рівнянь після підстановки знову одержимо лінійне однорідне диференціальне рівняння
, на підставі властивості 2 лінійних рівнянь після підстановки знову одержимо лінійне однорідне диференціальне рівняння 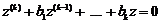 . Причому, оскільки
. Причому, оскільки 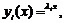 а
а 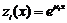 , то показники
, то показники 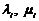 зв'язані співвідношенням
зв'язані співвідношенням 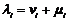 . Звідси кореню
. Звідси кореню 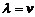 кратності
кратності 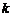 відповідає корінь
відповідає корінь 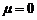 кратності
кратності 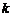 . Як випливає з попереднього пункту, кореню
. Як випливає з попереднього пункту, кореню 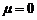 кратності
кратності 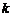 відповідає загальний розв’язок вигляду
відповідає загальний розв’язок вигляду 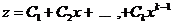 .
.
З огляду на те, що 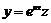 , одержимо, що кореню
, одержимо, що кореню 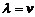 кратності
кратності 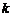 відповідає розв’язок
відповідає розв’язок 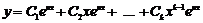 .
.
в) Нехай характеристичне рівняння має корені 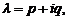
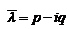 кратності
кратності 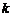 . Проводячи аналогічні викладки одержимо, що їм відповідають лінійно незалежні розв’язки
. Проводячи аналогічні викладки одержимо, що їм відповідають лінійно незалежні розв’язки
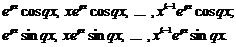
І загальним розв’язком, що відповідає цим кореням буде 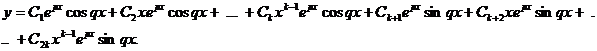
3. Знаходження частинного розв’язку лінійного неоднорідного рівняння n-го порядку за допомогою методу варіації довільної сталої.
 2018-01-21
2018-01-21 309
309








