Диференціальні рівняння першого порядку

Рівняння першого порядку, що розв’язане відносно похідної, має вигляд

.

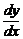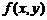Диференціальне рівняння становить зв’язок між коорди­натами точки та кутовим коефіцієнтом дотичної до графі­ку розв’язку в цій же точці. Якщо знати та , то можна обчислити тобто 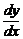. Таким чином, диференціальне рівняння визначає поле напрямків, і задача інтегрування рівнянь зводиться до знаходження кривих, що звуться інтегральними кривими, напрям дотичних до яких в кожній точці співпадає з напрямом поля.

Рівняння вигляду , або більш загального вигляду

називаються рівняннями зі змінними, що розділяються. Розділимо його на і одержимо

. Взявши інтеграли, отримаєм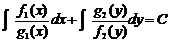о , або .

Визначення. Кінцеве рівняння , що визначає розв’язок диференціального рівняння як неявну функцію від , називається інтегралом розглянутого рівняння.

Визначення. Рівняння , що визначає всі без винятку розв’язки даного диференціального рівняння, називається загальним інтегралом.

Бувають випадки (в основному), що невизначені інтеграли або не можна записати в елементарних функціях. Незважаючи на це, задача інтегрування вважається виконаною. Кажуть, що диференціальне рівняння розв’язане в квадратурах.

Можливо, що загальний інтеграл розв’язується відносно : . Тоді, завдяки вибору , можна одержати всі розв’язки.

Визначення. Залежність , що тотожньо задовольняє вихідному диференціальному рівнянню, де довільна стала, називається загальним розв’язком диференціального рівняння.

Геометрично загальний розв’язок являє собою сім’ю кривих, що не перетинаються, які заповнюють деяку область. Іноді треба виділити одну криву сім’ї, що проходить через задану точку .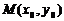

Визначення. Знаходження розв’язку , що проходить через задану точку 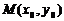, називається розв’язком задачі Коші.

Визначення. Розв’язок, який записаний у вигляді і задовольняє умові 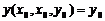, називається розв’язком у формі Коші.

Визначення. Простір називається метричним, якщо для довільних двох точок визначена функція , що задовольняє аксіомам:

1. 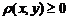, причому тоді і тільки тоді, коли ;

2. (комутативність);

3. (нерівність трикутника).

Функція називається відстанню в просторі (метрикою простору ).

Приклад 1.6.1. Векторний 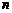- вимірний простір .

Нехай . За метрику можна взяти: , .

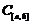Приклад 1.6.2. Простір неперервних функцій на відрізку позначається - . За метрику можна взяти

Визначення. Послідовність називається фундаментальною, якщо для довільного 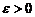існує таке, що при 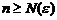і довільному буде .

Визначення. Метричний простір називається повним, якщо довільна фундаментальна послідовність точок простору збігається до деякої точки простору .

Теорема (принцип стискуючих відображень). Нехай в повному метричному просторі задано оператор , що задовольняє умовам.

1. Оператор переводить точки простору в точки цього ж простору, тобто якщо , то і .

2. Оператор є оператором стиску, тобто , де - довільні точки .

Тоді існує єдина нерухома точка , яка є розв’язком операторного рівняння і вона може бути знайдена методом послідовних відображень, тобто , де , причому , вибирається довільно.