Методи побудови функції Ляпунова

До цього часу не існує конструктивних методів побудови функцій Ляпунова.

1. Розглянемо систему на площині:

Функцію Ляпунова шукаємо у вигляді: 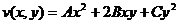квадратичної форми. Якщо форма додатньо визначена, то лінії рівня α являють собою еліпси. Виберемо коефіцієнти A, B, C таким чином, щоб зодовольняли умовам ,тобто виконувалась друга теорема Ляпунова.

Звідси маємо:

Прирівнюючи коефіцієнти при однакових степенях одержимо: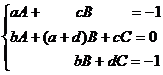

Звідси: , , ,

Умовою асимптотичної стійкості є (за критерієм Сільвестра)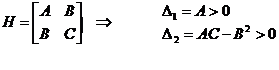

2. Для систем загального вигляду 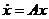, . Функція Ляпунова шукається у вигляді загальної квадратичної форми: 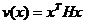, де симетрична додатньо визначена матриця. Її похідна

Якщо прирівняти похідну від’ємно визначеній квадратичній формі , де - додатньо визначена матриця, то знаходження функції Ляпунова 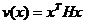зводиться до розв’ язання матричного рівняння

Доведено, що якщо А – асимптотично стійка (тобто ), то при довільній додатньо визначеній матриці С матриця рівняння Ляпунова має єдиний розв’язок – додатньо визначену матрицю Н.

Таким чином існування квадратичної функції Ляпунова є необхідною і достатньою умовою асимптотичної стійкості лінійної стаціонарної системи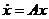

3. Рівняння коливання , - сила тертя, - відновлююча сила.

Заміна . Тоді рівняння перейде в систему

Функцію Ляпунова беремо у вигляді повної енергії

Повна похідна

І умова стійкості точки спокою х=0, у=0 є f(x)x>0, g(x)>0.

1. Метод лінійного наближення є простим. Недоліком є наявність критичних випадків і неможливість оцінки області стійкості.
2. Метод функції Ляпунова є (взагалі кажучи) необхідною і достатньою умовою стійкості. Причому він дозволяє оцінити область стійкості. Але побудова функції Ляпунова є в загальному випадку проблемою.