Теорема(Критерій Гурвіця)

12 13 14 15 16 17 18

Щоб лін стац сист була асимптот стійкою <=>щоб усі головні діагон мінори мат Гурвіця були додатні. Тобто ∆1 =р>0

∆2 = │р1 1│>0

│р3 р2│

............

∆n=рn∆n-1>0 (без доведення)

Теорема(Критерій Стодолі)

Якщо поліном n-го порядку має корені з від’ємною дійсною частиною (Re λi(А)<0) =>всі коєф полінома додатні(рі>0,і=1,n).

Заув: Для n=2 тобто f2(λ)= λ²+р1λ+р2 необхід умова асимптот стійкості (Стодолі) співпадає з необх і достат умовами асим стійкості(Гурвіця).

В техніці частіше частотні крит стійк. Одним з них є крит Михайлова. На підставі хар рів

λⁿ+р1λⁿֿ¹+...+рn=0 склад функц комплексного аргум f(z)=zⁿ+p1zⁿֿ¹+…pn-1z+pn.В комплексній площині будуємо графік функц: f(iw)=(iw)ⁿ+p1(iw)ⁿֿ¹+…+pn.

При зміні 0≤w<+∞ в площині { Re f, Im f}будуеться крива, що наз подографом Михайлова.

Теорема (критерій Михайлова): Щоб характеристичний поліном мав корені з від’ємними дійсними частинами (Re l < 0) необхідно і достатньо, щоб приріст аргументу

7.Метод функцій Ляпунова. Основні визначення та теореми

Другий метод Ляпунова

При дослідженні нелінійних систем поширення набуває другий метод Ляпунова. Суть його плягає в тому, що виснвок про стійкість робиться на підставі поведінки деякої наперед вибраної функції вздовж розв’язку системи.

Інтерпритація: Очевидно, що стійкий стан рівноваги кульки буде там, де енергія мінімальна. Причому вздовж інших розв’язків вона повинна зменшуватись.

Основні визначення

Визначення 1: Функція u(x) називається додатньо-постійною, якщо u(0) = 0 і u(x) > 0 при x ≠ 0.

Визначення 2: Функція u(x,t), t t називається додатньо-визначеною, якщо існує додатньо-постійною функція W(x) така, що u(x,t) W(x) і u(0,t) = 0.

Визначення 3: Функція u(x,t) має нескінченно малу вищу границю, якщо існує додатньо- постійна функція W (x) така, що u(x,t) W (x), u(0,t) = 0.

/////////////////Додаткові визначення /////////////////////////////////////////////////////////////

Визначення Ф-цію Ляпунова V(x)=V(х₁,х₂,...,х_n) наз. додатньовизначеною (від’ємновизначеною) на множині , якщо на цій множині V(x)>0 (V(x)<0) коли х 0 і V(0)=0.

Визначення. Ф-цію V(x) наз. додатньопостійною (від’ємнопостійною) на множині , якщо на цій множині V(x) 0 (V(x) 0)

Визначення. Ф-ція V(x) в околі т. х=0 не є знаковизначеною, якщо вона в цьому околі приймає як додатні, так і від’ємні значення.

Визначення. Повною похідною ф-ції V(х₁,х₂,...,х_n) в силу с-ми д/р наз вираз .

Озн. Ф-ція V(х₁,х₂,...,х_n,t) має нескінченно малу вищу границю, якщо існує додатньовизначена ф-ція W(х₁,х₂,...,х_n) при якій V(х₁,х₂,...,х_n,t) <=W(х₁,х₂,...,х_n), V(0,0,...,0,t) 0, t t₀ /

////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

Геометрично:

Якщо нескінченно мала вища границя

ДОВЕДЕННЯ

Як випливає з залежності загального розв’язку,його вигляд записується у формі:

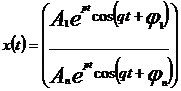якщо корені дійсні,різні, ,якщо

комплексний корінь і

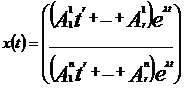,якщо -кратні корені.

v(x,t) = має неск. малу вищу границю, але не е додотньо постійною.

v(x,t) = не має неск малу вищу границю.

Визн 4: Похідну вигляду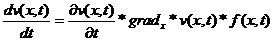

()

називається похідною функції v(x,t) в силу системи (вздовж розв. системи по напрямку

векторного поля).

Теорема (Перша теорема Ляпунова про стійкість):

Нехій існує непер-дифер. функція v(x,t), що задов. умовам:

1: Функція v(x,t) додатньо визначеною: v(x,t) W(х), v(0,t)=0, W(0)=0

2: Похідна функції v(x,t) в силу системи недодатня

Тоді нульовий розв’язок х(t) = 0 системи стійкий за Ляпуновим.

За умовою функція v(x,t) додатньо визначеною. Тобто існує v(x,t) W(х) > 0.

Візьмемо довільне 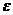>0 і розглянемо 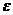- окіл початку координат

Функція W(х) неперервна W(0) = 0. Тому існує :

W(х) > , х є .Фіксуємо .

Поскільки функція v(x,t 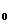) - неперервна

то існує - окіл початку координат,

в якому v(x,t 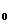) > .Розглянемо розв.

x(t) системи, що починається в -

околі, тобто є .Покажемо, що

він не досягне 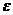- границі. Нехай від

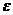супротивного існує t : |x(t )| = . Але
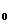тоді повинно існувати : t < t

таке, що v(x(), ) = . За умовою похідна функції v(x,t) недодатня, тобто вздовж розв. функція не збільш. І одержали

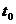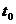< v(x(), ) v(x(), ) = (за вибором x()).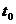

Таким чином припущення, що існує t : | | = 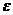невірне і | | < 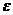, t .

Тобто розв. = 0 стійкий за Ляпуновим

Більш сильною є друга теорема Ляпунова.

Теорема (2-га теорема Ляпунова про асимптотичну стійкість):

Нехай існує неперервна диференційовна функція v(x,t), що задовольняє умовам:

1: v(x,t) – додатньо визначеною??

2: v(x,t) має нескінчено малу вищу границю

3: повна похідна її в силу системи від’ємно визначена < 0, v(x,t) W(х)

Тоді нульовий розв’язок асимптотично стійкий.

При дослідженні нестійкості використовують дві теореми Ляпунова про стійкість і

теорему Четаєва.

Теорема (Четаєва про стійкість):

Нехай існує неперервна диференційовна функція v(x,t), область додатньості якої

містить початок координат, П(x,t) = {(x,t): v(x,t) >0} є (0; 1) і має властивості:

1: Функція v(x,t) - обмежена по

2: В області П(x,t): > 0

3: Там де v(x,t) > => >0 (рівном по часу )

Теорема Ляпунова і Четаєва допускають просту геометричну інтерпретацію.

Перша теорема означає, що існує всюди щільна ситтема околів v(x,t) = і векторне поле сист. нправлене всередину(або дотикається) до сім’ї v(x,t) = .

v(x,t) – додатньо визначена

Якщо v(x,t) - додатньо визначена функція, то лінії рівня

v(x,t) = являють собою замкнені поверхні

Перша теорема Ляпунова стверджує, що , тобто векторне поле системи або направлене всередину, або дотикається. І траєкторії системи не виходять за межі цих поверхонь.

Друга теорема Ляпунова стверджує, що векторне поле направлене строго всередину 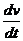<0. І траєкторії входять „строго” всередину.(див. рис.1)