| Номер четверти | Код

| Процент отличных оценок | Составляющие | ||||

| 
| 
| 
| 
| 
| ||
| I II III IV | 40.0 58.3 70.8 91.5 | 28.16 54.47 75.39 85.86 | 11.84 3.83 -4.59 5.64 | 29.6 6.57 -6.48 6.16 | 28.2 54.5 75.5 91.3 | 0.0 0.0 0.1 5.4 | |
| I II III IV | 67.9 53.6 80.4 100.0 | 68.84 54.70 77.71 102.92 | -0.94 -1.10 2.69 -2.92 | -1.38 -2.05 3.35 -2.92 | 102.4 109.6 113.6 114.9 | 33.6 54.9 35.9 11.9 |
Таблица 3.9
Изменение процента учащихся, получивших оценку "отлично" по четвертям
В экспериментальных группах за отдельные годы обучения
Коды
 , , 
| Классы 10а | Классы 11а | ||||||

| 
| 
| 
| 
| 
| 
| 
| |
| 40.0 58.3 70.8 91.5 | 38.36 58.40 74.67 88.89 | 1.64 -0.10 -3.87 2.61 | 4.10 0.17 5.46 2.85 | 67.9 53.6 80.4 100.0 | 67.9 53.6 80.4 100.0 | -0.00 -7.1*10-15 -0.00 -1.4*10-10 | -0.00 -0.00 -0.00 -0.00 |
Из данных таблицы 3.9 видно, что точность формулы (3.6) достаточно высока, а выражение (3.7) характеризуется как функциональная математическая зависимость.
Далее была сделана попытка усложнения конструкции статистической модели с тем, чтобы попытаться повысить её точность (снизить максимальную относительную погрешность).
После идентификации была получена формула
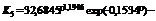

 , (3.8)
, (3.8)
которая уже имеет малую погрешность (табл. 3.10).
Здесь появилась третья составляющая, которая имеет волновую синусоидальную зависимость и тем самым характеризует неустойчивость знаний высокого уровня во времени. При этом эта волна затухающая, а затухание происходит по экспоненциальной зависимости. Половина периода волны равна 2,0388, то есть длина волны равна почти четырем четвертям, то есть чуть больше одного учебного года.
Таблица 3.10
Изменение процента учащихся, получивших оценку "отлично" по четвертям
 2018-01-21
2018-01-21 590
590








