Задача 1. Найти максимум целевой функции L =-x+2y при следующих ограничениях:
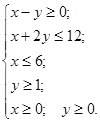
Решить задачу при дополнительном условии (ДУ):
ДУ: Найти минимум целевой функции L=3x+y при тех же ограничениях.
Решение:
Решим неравенство графическим способом. Введем на плоскости прямоугольную систему координат 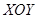 , в которой точки с координатами
, в которой точки с координатами 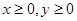 находятся в первом квадранте этой координатной плоскости.
находятся в первом квадранте этой координатной плоскости.
Графическое решение неравенства типа 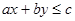 определяет одну из полуплоскостей, на которые прямая
определяет одну из полуплоскостей, на которые прямая 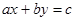 делит координатную плоскость. Решением неравенства будет та полуплоскость все точки которой будут ему удовлетворять.
делит координатную плоскость. Решением неравенства будет та полуплоскость все точки которой будут ему удовлетворять.
Исходя из этого, рассмотрим каждое, из приведенной выше системы, неравенство. Решением каждого из них будет соответствующая ему полуплоскость, а решением системы будет область, образованная пересечением всех найденных полуплоскостей. Графическое решение нашей системы приведено на рисунке 1. Здесь прямая (1), соответствует уравнению 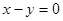 . Построена она по двум точкам (
. Построена она по двум точкам (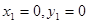 ) и (
) и (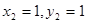 ) и точка О(2,1), удовлетворяющая нашему первому неравенству
) и точка О(2,1), удовлетворяющая нашему первому неравенству 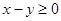 , определяет в качестве решения полуплоскость,лежащую ниже прямой (1). Аналогично решением второго неравенства
, определяет в качестве решения полуплоскость,лежащую ниже прямой (1). Аналогично решением второго неравенства 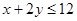 является полуплоскость, лежащая ниже прямой (2), соответствующей уравнению
является полуплоскость, лежащая ниже прямой (2), соответствующей уравнению 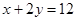 , решением третьего неравенства является полуплоскость, находящаяся слева от прямой (3) -
, решением третьего неравенства является полуплоскость, находящаяся слева от прямой (3) - 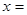 6, а решением четвертого, полуплоскость выше прямой (4)-
6, а решением четвертого, полуплоскость выше прямой (4)- 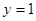 .Решением же системы является в нашем случае область АВСД, которая была образована пересечением четырех, выше найденных полуплоскостей. Область АВСД образует область допустимых решений или допустимых планов нашей задачи, в которой мы и будем искать оптимальное решение L=
.Решением же системы является в нашем случае область АВСД, которая была образована пересечением четырех, выше найденных полуплоскостей. Область АВСД образует область допустимых решений или допустимых планов нашей задачи, в которой мы и будем искать оптимальное решение L= 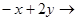 max. Для этого построим вектор
max. Для этого построим вектор 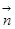 = grad L(x,y), который укажет направление наибольшего возрастания целевой функции.
= grad L(x,y), который укажет направление наибольшего возрастания целевой функции.
Рисунок 1.

Линии, перпендикулярные этому вектору - L(x,y)=const, которые называются линиями уровня, задают одно из возможных значений целевой функции. На графике одно из этих уравнений, например L=-x+2y=6, задает прямую, которой соответствует значение L=6. Максимальное же значение целевой функции будет соответствовать, такой линии уровня, которая будет получена путем параллельного переноса одной из линий уровня, проходящей через область допустимых планов АВСД, в пограничную область АВСД в направлении вектора 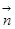 =(-1,2)=grad L. В нашем случае максимум целевой функции достигается в точке В, которая является точкой пересечения прямых 1 и 2. Решив систему уравнений, соответствующих этим прямым:
=(-1,2)=grad L. В нашем случае максимум целевой функции достигается в точке В, которая является точкой пересечения прямых 1 и 2. Решив систему уравнений, соответствующих этим прямым:
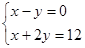
получим координаты точки В=(4,4) и Lmax=-4+2x4=4.
Аналогично будем искать минимум целевой функции L=3x+у.
Для этого построим вектор 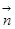 =grad L=(3,1) и одну из линий уровня L, имеющую уравнение 3x+1=6 (см. рисунок 2).
=grad L=(3,1) и одну из линий уровня L, имеющую уравнение 3x+1=6 (см. рисунок 2).
Рисунок 2
Далее будем параллельно перемещать ее в направлении, противоположном направлению вектора 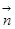 (3,1) до границы области допустимых планов АВСД. Последней точкой этой области, через которую проходит наша прямая L и в которой она достигает своего минимального значения будет точка А. Эта точка является пересечением прямых 1 и 3. Решив систему уравнений, соответствующих этим прямым:
(3,1) до границы области допустимых планов АВСД. Последней точкой этой области, через которую проходит наша прямая L и в которой она достигает своего минимального значения будет точка А. Эта точка является пересечением прямых 1 и 3. Решив систему уравнений, соответствующих этим прямым:
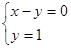
получим координаты этой точки А=(1,1) и Lmin=3x1+1=4.
Задача 2.
Для изготовления изделия А и В предприятие использует три вида сырья. На производство одного изделия А, требуется 2 единицы сырья первого вида и 2 единицы – второго, а на производство одного изделия В соответственно 3 единицы первого, 1 единица второго и 3 единицы третьего. Производство обеспечено сырьем первого вида в количестве 19 единиц, второго - 13 единиц и третьего - 15.Производство одного изделия А дает предприятию 7 млн. руб. прибыли, а изделие В – 5 млн. руб. прибыли. Составить план производства изделий А и В, максимизирующий общую прибыль предприятия.
Решение:
Сведения из задачи о количестве ресурсов, необходимых для производства единицы каждого товара, обеспеченности предприятия этими ресурсами и размерах прибыли, данной каждым из товаров представим в виде следующей таблицы:
| Ресурсы | Товары А В | Запас ресурсов | |
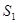 | |||
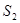 | |||
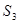 | |||
| Прибыль |
Составим план производства изделий А и В, максимизирующий общую прибыль предприятия.
Обозначим через 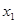 и
и 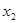 запланированный объем производства товаров А и В. Из экономического смысла величин
запланированный объем производства товаров А и В. Из экономического смысла величин 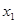 и
и 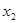 следует, что
следует, что 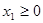 ,
, 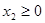 . Тогда, учитывая количество единиц ресурсов, затрачиваемых при производстве товаров А и В, а также запасы этих ресурсов, получим следующую систему ограничений:
. Тогда, учитывая количество единиц ресурсов, затрачиваемых при производстве товаров А и В, а также запасы этих ресурсов, получим следующую систему ограничений:
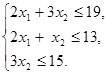
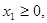
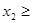 0
0
При этом реализация товаров А и В дает прибыль:
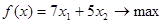
Функция 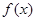 - называется целевой функцией, которая совместно с описанной выше системой ограничений представляет собой математическую модель приведенной задачи. Решим ее симплекс-методом.
- называется целевой функцией, которая совместно с описанной выше системой ограничений представляет собой математическую модель приведенной задачи. Решим ее симплекс-методом.
В начале приведем нашу задачу к канонической форме. Для этого от системы неравенств перейдем к системе линейных уравнений, введя дополнительные переменные: 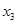 ,
, 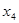 ,
, 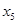 , экономический смысл которых заключается в том, что это остатки ресурсов при производстве товаров А и В. В итоге получим следующую задачу:
, экономический смысл которых заключается в том, что это остатки ресурсов при производстве товаров А и В. В итоге получим следующую задачу:
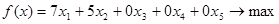
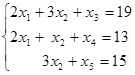
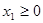 ,
, 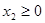 ,
, 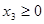 ,
, 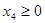 ,
, 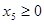 .
.
Проведем решение с помощью симплексных таблиц. Первая симплексная таблица имеет вид:
Таблица 1
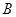 | 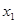 | 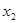 | 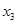 | 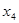 | 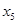 | 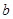 | 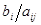 |
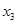 | 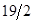 | ||||||
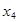 | 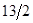 | ||||||
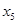 | - | ||||||
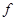 | -7 | -5 |
Здесь 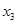 ,
, 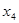 ,
, 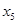 - базисные переменные (именно в этом порядке столбцы образуют единичный базис) и заполняют столбец ”
- базисные переменные (именно в этом порядке столбцы образуют единичный базис) и заполняют столбец ” 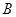 ”
”
нашей симплексной таблицы. А переменные 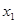 и
и 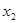 - свободные
- свободные
Вектор 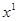 = (0,0,19,13,15), является начальным решением нашей исходной задачи. Значение целевой функции на этом плане -
= (0,0,19,13,15), является начальным решением нашей исходной задачи. Значение целевой функции на этом плане - 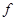 (
(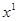 )=0.
)=0.
Сформулируем правило заполнения последней строки, которая называется индексной. В индексной строке записываются коэффициенты целевой функции с противоположным знаком (эти числа называются оценками опорного плана), и ее значение (в столбце 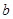 ).
).
Решение задачи начинается с анализа индексной строки. Наличие отрицательных оценок 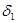 =-7 и
=-7 и 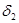 =-5 означает, что этот опорный план -
=-5 означает, что этот опорный план - 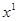 не является оптимальным. Выбор минимальной из отрицательных оценок, которой в нашем случае будет
не является оптимальным. Выбор минимальной из отрицательных оценок, которой в нашем случае будет 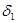 =-7 позволяет определить разрешающий столбец -
=-7 позволяет определить разрешающий столбец - 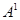 и переменную -
и переменную - 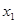 , которую будем вводить в базис, а выбор мини-мальной из оценок
, которую будем вводить в базис, а выбор мини-мальной из оценок 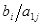 ,которой будет min
,которой будет min 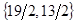 =
= 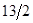 позволяет определить разрешающую строку
позволяет определить разрешающую строку 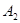 и переменную
и переменную 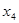 , которую выведем из базиса, для того чтобы получить новый опорный план. На пересечении выделенных серым цветом в таблице 1 разрешающего столбца -
, которую выведем из базиса, для того чтобы получить новый опорный план. На пересечении выделенных серым цветом в таблице 1 разрешающего столбца - 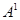 и разрешающей строки
и разрешающей строки 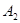 находится разрешающий элемент
находится разрешающий элемент 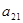 =2. Далее для перехода к новому базису применяется способ элементарных преобразований метода Гаусса. При этом в преобразование включается и индексная (последняя) строка симплексной таблицы в результате чего происходит вычисление новых оценок. После несложных действий, а именно, делим разрешающую строку на “2” и последовательно умножая полученную новую разрешающую строку на “-2” и складывая с первой и затем на “7” и складывая с последней (третья строка при этом в нашем случае останется без изменений) - получаем следующую таблицу:
=2. Далее для перехода к новому базису применяется способ элементарных преобразований метода Гаусса. При этом в преобразование включается и индексная (последняя) строка симплексной таблицы в результате чего происходит вычисление новых оценок. После несложных действий, а именно, делим разрешающую строку на “2” и последовательно умножая полученную новую разрешающую строку на “-2” и складывая с первой и затем на “7” и складывая с последней (третья строка при этом в нашем случае останется без изменений) - получаем следующую таблицу:
Таблица 2
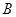 | 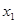 | 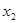 | 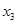 | 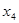 | 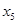 | 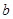 | 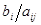 |
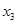 | -1 | 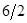 =3 =3 | |||||
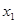 | 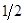 | 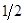 | 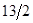 | 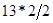 =13 =13 | |||
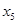 | 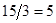 | ||||||
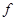 | - 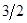 | 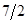 | 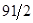 |
Новый опорный план 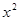 =(13, 2, 3, 0, 15/3) невырожденный, но и неоптимальный, так в последней строке симплексной таблицы 2 имеется отрицательная оценка
=(13, 2, 3, 0, 15/3) невырожденный, но и неоптимальный, так в последней строке симплексной таблицы 2 имеется отрицательная оценка 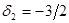 . Значение целевой функции на этом плане -
. Значение целевой функции на этом плане - 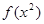 =91/2. Из анализа таблицы 2 следует, что новой базисной переменной нужно сделать
=91/2. Из анализа таблицы 2 следует, что новой базисной переменной нужно сделать 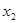 . А сравнивая отношения
. А сравнивая отношения 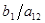 =3,
=3, 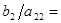 13 и
13 и 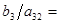 5, заключаем, что из базиса нужно вывести переменную
5, заключаем, что из базиса нужно вывести переменную 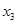 . Очередная таблица будет иметь вид:
. Очередная таблица будет иметь вид:
Таблица 3
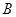 | 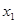 | 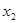 | 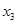 | 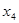 | 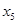 | 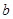 | 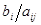 |
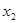 | 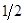 | - 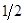 | |||||
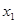 | - 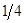 | 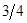 | |||||
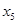 | - 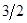 | 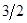 | |||||
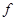 | 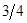 | 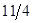  |
Третий опорный план 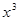 =(5,3,0,0,6) – оптимальный (отрицательных оценок в нижней строке таблицы больше нет). Так как нулевых оценок в столбцах свободных переменных (на данном опорном плане это -
=(5,3,0,0,6) – оптимальный (отрицательных оценок в нижней строке таблицы больше нет). Так как нулевых оценок в столбцах свободных переменных (на данном опорном плане это - 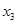 и
и 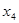 ) нет, то найденное оптимальное решение единственное. Оптимальное значение целевой функции
) нет, то найденное оптимальное решение единственное. Оптимальное значение целевой функции 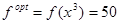 .
.
Следовательно оптимальным планом, дающим максимальную прибыль в 50 единиц является производство 5 единиц товара А и 3 единиц товара В. Решение задачи закончено.
Задача 3.
| По\Пн | 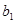 =28 =28 | 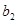 =17 =17 | 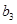 =28 =28 | 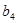 =20 =20 |
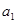 =15 =15 | 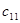 =7 =7 | 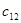 =3 =3 | 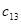 =4 =4 | 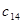 = =  2 2 |
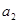 =31 =31 | 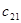 =6 =6 | 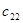 =1 =1 | 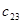 =4 =4 | 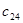 =6 =6 |
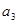 =25 =25 | 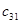 =6 =6 | 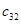 =9 =9 | 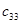 =5 =5 | 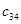 =3 =3 |
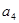 =22 =22 | 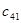 =10 =10 | 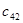 =4 =4 | 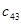 =7 =7 | 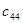 =9 =9 |
В 4 пунктах отправления (По) имеется однородный груз в количествах 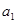 =15,
=15, 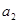 =31,
=31, 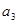 =25,
=25, 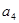 =22. Груз нужно перевести в 4 пункта назначения (Пн), потребности которых равны -
=22. Груз нужно перевести в 4 пункта назначения (Пн), потребности которых равны - 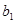 =28,
=28, 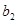 =17,
=17, 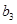 =28,
=28, 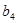 =20. Стоимость перевозки единицы груза из i – го По в j – ый Пн равна
=20. Стоимость перевозки единицы груза из i – го По в j – ый Пн равна 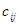 .
.
Требуется составить план перевозки грузов из По в Пн, при котором суммарные расходы на перевозку будут минимальными.
Решение:
Решение транспортной задачи начинается с нахождения первого опорного плана. Существует несколько методов построения опорного плана перевозок. Рассмотрим один из них – метод наименьшей стоимости.
В опорном плане должно быть n+m-1, базисных переменных, а значит в таблице столько же занятых клеток, где n – количество По, а m – Пн. В нашем случае n+m-1=4+4-1=7, значит столько заполненных клеток должно быть в нашей транспортной таблице.
При построении опорного плана методом наименьшей стоимости первой заполняется клетка с минимальной стоимостью. При этом либо удовлетворяется заявка соответствующего Пн, либо исчерпывается запас По.
В нашей задаче минимальную стоимость - 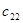 =1 мы имеем в клетке (
=1 мы имеем в клетке (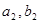 ). За счет запаса По
). За счет запаса По 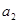 =31 можно удовлетворить всю заявку Пн
=31 можно удовлетворить всю заявку Пн 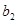 =17. Поэтому записываем 17 в клетку (
=17. Поэтому записываем 17 в клетку (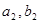 ). При этом заявка Пн -
). При этом заявка Пн - 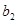 теперь полностью удовлетворена. Но надо запомнить, что запас По-
теперь полностью удовлетворена. Но надо запомнить, что запас По- 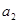 уменьшился на 17 единиц и теперь составляет 14 единиц. Следующую по величине стоимость равную
уменьшился на 17 единиц и теперь составляет 14 единиц. Следующую по величине стоимость равную 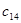 =2 мы имеем в клетке (
=2 мы имеем в клетке (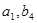 ). Но поскольку запас По-
). Но поскольку запас По- 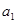 =15, что меньше заявки Пн-
=15, что меньше заявки Пн- 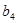 =20, в эту клетку мы можем записать только 15 единиц товара. При этом запас По-
=20, в эту клетку мы можем записать только 15 единиц товара. При этом запас По- 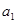 =15 полностью исчерпан, но помним, в Пн -
=15 полностью исчерпан, но помним, в Пн - 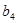 необходимо доставить еще 5 единиц товара, используя возможности оставшихся По. Так как в клетке (
необходимо доставить еще 5 единиц товара, используя возможности оставшихся По. Так как в клетке (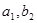 ) имеющей следующую по величине стоимость
) имеющей следующую по величине стоимость 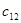 =3, уже стоит прочерк, то далее будет заполнена клетка (
=3, уже стоит прочерк, то далее будет заполнена клетка (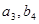 ) с такой же стоимостью
) с такой же стоимостью 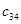 =3, куда мы запишем оставшиеся для полного выполнения заявки 5 единиц товара. Рассуждая аналогично заполняем остальные клетки в такой последовательности:
=3, куда мы запишем оставшиеся для полного выполнения заявки 5 единиц товара. Рассуждая аналогично заполняем остальные клетки в такой последовательности:
(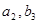 ), (
), (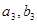 ), (
), (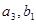 ), (
), (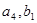 ).Нетрудно убедиться, что сумма перевозок в каждой строке равна запасу соответствующего По, а в каждом столбце – заявке соответствующего Пн. В результате получим следующую транспортную таблицу соответствующую первому опорному плану:
).Нетрудно убедиться, что сумма перевозок в каждой строке равна запасу соответствующего По, а в каждом столбце – заявке соответствующего Пн. В результате получим следующую транспортную таблицу соответствующую первому опорному плану:
| .По\Пн | 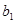 =28 =28 | 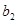 =17 =17 | 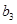 =28 =28 | 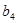 =20 =20 |
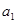 =15 =15 | - | - | - | |
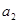 =31 =31 | - | - | ||
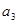 =25 =25 | - | |||
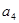 =22 =22 | - | - | - |
Сам первый опорный имеет вид- 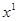 =(0,0,0,15,0,17,14,0,6,0,14,0,14,5,22,0,0,0).
=(0,0,0,15,0,17,14,0,6,0,14,0,14,5,22,0,0,0).
А целевая функция задачи на этом плане равна
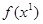 =15х2+17х1+14х4+6х6+14х5+5х3+22х10=444.
=15х2+17х1+14х4+6х6+14х5+5х3+22х10=444.
Этот план можно улучшить, т.е. уменьшить стоимость перевозок за счет другого распределения товара в клетках. Для этого в пустую клетку помещается товар 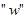 и далее, осуществляя его переброску по замкнутому циклу, используя только базисные, т.е. заполненные клетки, получаем новое распределение заполненных клеток, соответствующих плану с новой стоимостью перевозок, отличной от старой на величину
и далее, осуществляя его переброску по замкнутому циклу, используя только базисные, т.е. заполненные клетки, получаем новое распределение заполненных клеток, соответствующих плану с новой стоимостью перевозок, отличной от старой на величину 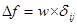 .Цикл – это замкнутая ломаная из горизонтальных и вертикальных отрезков, соединяющая несколько клеток таблицы и совершающая в каждой из них поворот на 90 градусов. Две последовательные вершины цикла лежат либо в одной строке, либо в одном столбце. В одной из них объем перевозки товара увеличивается (в клетке ставится знак +), в другой уменьшается на столько же единиц (в клетке ставится знак -), а
.Цикл – это замкнутая ломаная из горизонтальных и вертикальных отрезков, соединяющая несколько клеток таблицы и совершающая в каждой из них поворот на 90 градусов. Две последовательные вершины цикла лежат либо в одной строке, либо в одном столбце. В одной из них объем перевозки товара увеличивается (в клетке ставится знак +), в другой уменьшается на столько же единиц (в клетке ставится знак -), а 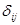 является оценкой этой клетки. Очевидно, что уменьшение стоимости будет только в том случае, если мы перебросим товар в пустую клетку с отрицательной оценкой.
является оценкой этой клетки. Очевидно, что уменьшение стоимости будет только в том случае, если мы перебросим товар в пустую клетку с отрицательной оценкой.
Существует метод, который позволяет автоматически находить клетки, для которых оценка 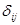 будет отрицательной. Этот метод называется методом потенциалов Он состоит в следующем. Предположим, что мы построили первый опорный план перевозок. Далее сопоставим каждому По – число
будет отрицательной. Этот метод называется методом потенциалов Он состоит в следующем. Предположим, что мы построили первый опорный план перевозок. Далее сопоставим каждому По – число 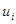 и каждому Пн – число
и каждому Пн – число 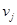 так, чтобы для любой базисной клетки выполнялось условие:
так, чтобы для любой базисной клетки выполнялось условие: 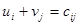 . Числа
. Числа 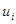 и
и 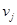 называются потенциалами. Оценки -
называются потенциалами. Оценки - 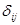 , вычисляются для пустых клеток по формуле
, вычисляются для пустых клеток по формуле 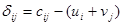 . Так как в нашем опорном плане m+n-1=4+4-1=7 базисных переменных, то для нахождения потенциалов нужно решить систему из 7 уравнений с 8-ю неизвестными. Поскольку число неизвестных на 1 больше числа уравнений значение одного потенциала можно выбрать произвольно. В нашей задаче система уравнений для нахождения потенциалов имеет вид:
. Так как в нашем опорном плане m+n-1=4+4-1=7 базисных переменных, то для нахождения потенциалов нужно решить систему из 7 уравнений с 8-ю неизвестными. Поскольку число неизвестных на 1 больше числа уравнений значение одного потенциала можно выбрать произвольно. В нашей задаче система уравнений для нахождения потенциалов имеет вид:
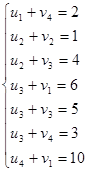
Полагаем 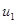 =0 и сразу получаем значения остальных потенциалов:
=0 и сразу получаем значения остальных потенциалов: 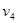 =2,
=2, 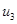 =1,
=1, 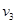 =4,
=4, 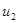 =0,
=0, 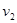 =1,
=1, 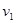 =5,
=5, 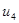 =5.
=5.
Теперь можно вычислить оценки:
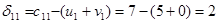
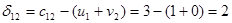 , аналогично
, аналогично 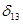 =0,
=0, 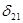 =1,
=1, 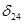 =4,
=4, 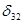 =7,
=7, 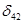 =-2,
=-2, 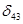 =-2,
=-2, 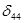 =-2. Данные оценки занесены в таблицу в свободные клетки слева от стоимостей перевозок и выделены серым цветом.
=-2. Данные оценки занесены в таблицу в свободные клетки слева от стоимостей перевозок и выделены серым цветом.
| .По\Пн | 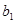 =28 =28 | 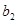 =17 =17 | 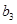 =28 =28 | 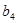 =20 =20 | 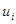 |
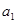 =15 =15 | 2 7 - | 2 3 - | 0 4 - | ||
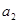 =31 =31 | 1 6 - | 4 6 - | |||
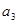 =25 =25 | 7 9 - | ||||
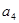 =22 =22 | -24 - | -2 7 - | -2 9 - | ||
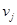 |
Для перехода к новому опорному плану свободная переменная с отрицательной оценкой вводится в базис, а одна из базисных переменных переводится в свободные. Для этого построим цикл с началом (и концом) в клетке (4,2) с отрицательной оценкой 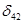 =-2 и вершинами в занятых клетках. Ребра цикла могут проходить и через свободные, и через занятые клетки, но повороты на 90 градусов должны происходить только в занятых клетках. В нашем примере получается следующий цикл:
=-2 и вершинами в занятых клетках. Ребра цикла могут проходить и через свободные, и через занятые клетки, но повороты на 90 градусов должны происходить только в занятых клетках. В нашем примере получается следующий цикл:
| .По\Пн | 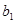 =28 =28 | 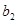 =17 =17 | 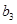 =28 =28 | 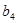 =20 =20 | 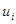 |
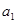 =15 =15 | 2 7 - | 2 3 - | 0 4 - | ||
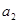 =31 =31 | 1 6 - | 4 6 - | |||
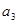 =25 =25 | 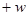 6 6  6 6 | 7 9 - | 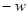 5 5 | ||
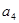 =22 =22 | 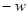 10 10 | -24 - | -27 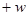 | -2 9 - | |
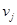 |
В начальной вершине цикла-клетка(4,3)помещаем символ “ 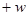 ”, в следующей вершине – клетка (3,3) ”
”, в следующей вершине – клетка (3,3) ” 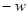 ”, потом – клетка (3,1) “
”, потом – клетка (3,1) “  ” и так далее по всем вершинам цикла: (4,3)
” и так далее по всем вершинам цикла: (4,3)  (3,3)
(3,3)  (3,1)
(3,1)  (4,1)(направление обхода не имеет значения). Значение клеток, отмеченных знаком “
(4,1)(направление обхода не имеет значения). Значение клеток, отмеченных знаком “ 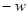 ”, уменьшается на величину
”, уменьшается на величину 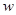 , а отмеченных знаком “
, а отмеченных знаком “ 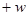 ” – увеличивается на ту же величину. Для вывода из базиса выбирается клетка, помеченная знаком “
” – увеличивается на ту же величину. Для вывода из базиса выбирается клетка, помеченная знаком “ 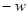 ” и имеющая наименьшее значение. Это условие гарантирует не отрицательность нового опорного плана. Если наименьшее значение находится в нескольких клетках, то выбирается любая из них. В любом случае значение целевой функции уменьшается на величину
” и имеющая наименьшее значение. Это условие гарантирует не отрицательность нового опорного плана. Если наименьшее значение находится в нескольких клетках, то выбирается любая из них. В любом случае значение целевой функции уменьшается на величину 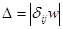 .
.
В данном примере 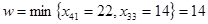 . Тогда новые значения переменных будут следующими:
. Тогда новые значения переменных будут следующими: 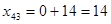 (и пустая клетка становится занятой),
(и пустая клетка становится занятой), 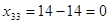 (занятая клетка становится пустой),
(занятая клетка становится пустой), 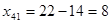 ,
, 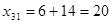 . Значение целевой функции на новом опорном плане будет равно
. Значение целевой функции на новом опорном плане будет равно 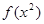 =444 - 2х14=416. Далее переходим к следующей таблице и вычисляем новые значения потенциалов и новые оценки, которые таким же образом заносим в эту таблицу.
=444 - 2х14=416. Далее переходим к следующей таблице и вычисляем новые значения потенциалов и новые оценки, которые таким же образом заносим в эту таблицу.
| .По\Пн |  =28 =28 | 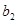 =17 =17 | 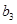 =28 =28 | 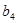 =20 =20 | 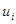 |
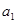 =15 =15 | 2 7 - | 4 3 - | 2 4 - | ||
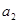 =31 =31 | -1 6  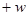 | 14 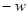 | 2 6 - | ||
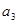 =25 =25 | 9 9 - | 2 5 | |||
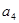 =22 =22 | 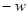 8 8 | 0 4 - | 14 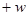 | - | |
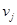 | -1 |
В результате проведенных вычислений обнаруживаем, что новый опорный план 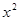 =(0,0,0,15,0,17,14,0,20,0,0,5,8,0,14,0) также не оптимален так как оценка
=(0,0,0,15,0,17,14,0,20,0,0,5,8,0,14,0) также не оптимален так как оценка 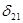 =-1, т.е. отрицательна и мы можем еще раз уменьшить значение нашей целевой функции. Построив цикл:(2,1)
=-1, т.е. отрицательна и мы можем еще раз уменьшить значение нашей целевой функции. Построив цикл:(2,1) 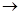 (2,3)
(2,3)  (4,3)
(4,3)  (4,1), для которого
(4,1), для которого 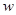 =8, получим новую таблицу и новое распределение товара, т.е. новый опорный план -
=8, получим новую таблицу и новое распределение товара, т.е. новый опорный план - 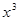 =(0,0,0,15,8,17,6,20,0,0,5,0,0,22,0). На этом опорном плане новое значение целевой функции будет равно -
=(0,0,0,15,8,17,6,20,0,0,5,0,0,22,0). На этом опорном плане новое значение целевой функции будет равно - 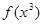 =416-1х8=408.
=416-1х8=408.
| .По\Пн | 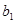 =28 =28 | 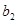 =17 =17 | 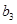 =28 =28 | 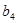 =20 =20 | 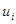 |
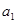 =15 =15 | 2 7 - | 3 3 - | 1 4 - | ||
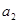 =31 =31 | 3 6 - | ||||
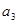 =25 =25 | 8 9 - | 1 5 - | |||
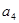 =22 =22 | 1 10 - | 0 4 - | 3 9 - | ||
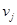 |
Новый же расчет потенциалов и соответствующих оценок показывает, что найденный нами план оптимален, так как среди оценок больше нет ни одной отрицательной. Однако, то обстоятельство, что оценка 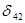 =0, говорит о том, что найденный опорный план не единственный. Построив цикл с вершинами в клетках (4,2)
=0, говорит о том, что найденный опорный план не единственный. Построив цикл с вершинами в клетках (4,2)  (2,2)
(2,2)  (2,3)
(2,3)  (4,3), можно получить еще один оптимальный опорный план
(4,3), можно получить еще один оптимальный опорный план 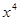 =(0,0,0,15,8,0,
=(0,0,0,15,8,0,
23,0,20,0,0,5,0,17,5,0) с тем же значением целевой функции.
Задача 4.(I вариант) Платёжная матрица имеет вид: 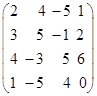
Найти цену игры и оптимальную стратегию.
Решение. Задана платёжная матрица размера (4х4). Набор чисел платёжной матрицы имеет смысл платы игрока В игроку А в зависимости от выбранных им стратегий. Стратегии игрока А – это строки матрицы. Стратегии игрока В – столбцы матрицы. Пусть стратегии игрока А нумеруются сверху вниз, а стратегии игрока В – слева направо. Задача игрока А – получить наибольший выигрыш, а задача игрока В – оказаться в наименьшем проигрыше. По правилам игры игрок А выбирает свою стратегию, не зная, какую стратегию выберет игрок В и наоборот: игрок В выбирает свою стратегию, не зная, какую стратегию выберет игрок А. В соответствии с определением, стратегия игрока А – строка чисел. Например, его вторая стратегия – это (3,5,-1,2): если при этом игрок В выбирает первую стратегию, то игрок В платит игроку А 3 ед., при выборе игроком В второй стратегии игрок А получит 5 ед., при выборе игроком В третьей стратегии игрок А платит 1 ед. и, наконец, игрок А получает 2 ед., если игрок В выбирает четвёртую стратегию. Если какая-то стратегия является предпочтительной по отношению к другой, то говорят, что та стратегия, которая более выгодная является доминирующей. Видно, что в заданной платёжной матрице вторая стратегия игрока А доминирует его первую, а третья его – доминирует четвёртую. Следовательно первую и четвёртую стратегии игрока А можно вычеркнуть. Аналогично заключаем, что четвёртая стратегия игрока В также может быть вычеркнута, так как её доминирует третья. В результате вычёркиваний приходит к платёжной матрице (2х3).
Попытаемся найти решение полученной после упрощений задачи в чистых стратегиях. Для этого справа в каждой строке выпишем гарантированный выигрыш игрока А, а внизу под каждым столбцом – максимальный проигрыш игрока В для каждой из стратегий:
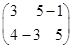
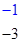
4 5 5
Договоримся считать, что теперь у игрока А имеется первая и вторая стратегии, а у игрока В – первая, вторая и третья (в оговоренном ранее порядке).
Для игрока А наилучшей является первая стратегия, так как он в наихудшем случае проигрывает 1 ед.: a0 =–1 – нижняя цена игры, а для игрока В наилучшей является первая стратегия, так как он в худшем случае платит 4 ед. = b0 верхняя цена игры. Так как нижняя и верхняя цены игры не совпадают, то в чистых стратегиях задача не имеет решения.
Найдём решение задачи в смешанных стратегиях. Для этого будем считать, что игрок А с вероятностью р использует первую стратегию и с вероятностью 1 – р – вторую.
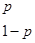
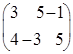
Найдём средний проигрыш игрока В.
Если игрок В выбирает первую стратегию, то он платит игроку А математическое ожидание проигрыша равное
u1=3p+4(1 – p)=4 – p
Если игрок В выбирает вторую стратегию, то он платит игроку А математическое ожидание проигрыша равное
u2=5p – 3(1 – p)=8p – 3
Если игрок В выбирает третью стратегию, то он платит игроку А математическое ожидание проигрыша равное
u3= – 1p+5(1 – p)=5 – 6p
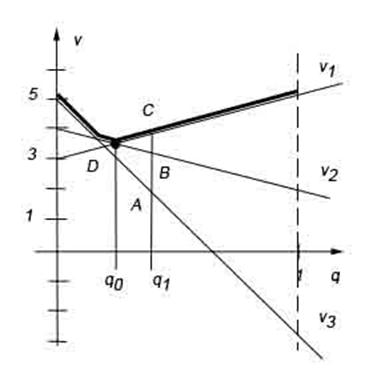
Так как неизвестной величиной является только одна – вероятность р, то проигрыш игрока В удобно изобразить на графике в переменных (u,p).
Изучим график. Если игрок А зафиксировал вероятность р1, то игрок В имеет возможность выбора стратегии из трёх вариантов: он выберет либо первую стратегию, тогда в среднем будет платить С единиц, либо вторую стратегию, тогда в среднем он будет платить К единиц, либо третью, тогда в среднем он будет платить В единиц. Естественно он заинтересован в наименьшей плате, поэтому он выберет стратегию 2.(точка К) Понимая это, игрок А захочет получить больший выигрыш и выберет другую вероятность, например, р2. Аналогичное рассмотрение этой вероятности игрока А и выбора игроком В платежей D, E, F, заключаем, что игрок В выберет опять стратегию 2 (точка D). Но при этом ему придётся платить больше, чем если бы игрок А выбрал вероятность р1. Из приведённого исследования видно, что для разных значений вероятности игрока А, платёж ему – это нижняя огибающая (выделенная жирная линия на рисунке). Тогда наилучший выбор для игрока А – это точка G.
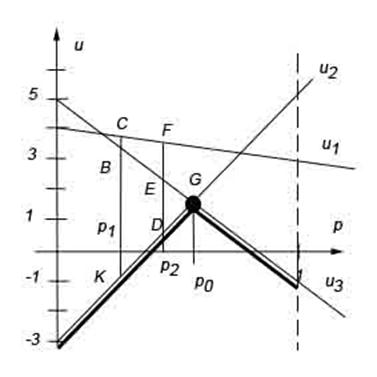
Найдём p0. Так как
 ,
,
то
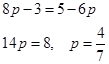
Найдём цену игры.
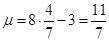
Найдём стратегии игрока В.
Точка G – точка оптимальной стратегии определяется как вторая и третья стратегии игрока В, поэтому первая и четвёртая стратегии игрока В не используются.
Пусть игрок В с вероятностью q использует стратегию 2 и с вероятностью (1 – q) – стратегию три. Но цена игры известна, поэтому можно написать уравнение на q в виде:
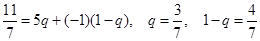
Ответ: Оптимальная стратегия матричной игры – смешанная. Игрок А не применяет первую и четвёртую стратегии, вторая стратегия им используется с вероятность 4/7, третья стратегия используется с вероятностью 3/7. Игрок В тоже не применяет первую и четвёртую стратегии, вторую применяет с вероятность 3/7, третью – с вероятностью 4/7. Цена игры равна 11/7.
Задача 4. (II вариант.) Платёжная матрица имеет вид: 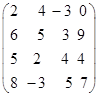 .
.
Найти цену игры и оптимальную стратегию.
Решение. Пусть как и в предыдущей задаче стратегии игрока А нумеруются сверху вниз, а стратегии игрока В – слева направо.. Видно, что в заданной платёжной матрице вторая стратегия игрока А доминирует его первую. Аналогично заключаем, что третья стратегия игрока В доминирует четвёртую и первую. В результате вычёркиваний приходит к платёжной матрице (3х2). Попытаемся найти решение задачи в чистых стратегиях. Для этого справа от каждой строки выпишем гарантированный выигрыш игрока А, а внизу под каждым столбцом – максимальный проигрыш игрока В для каждой из стратегий. В результате получим:
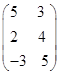
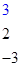
5 5
Договоримся считать, что теперь у игрока А имеется первая, вторая и третья стратегии, а у игрока В – первая и вторая.
Для игрока А наилучшей является первая стратегия, так как он в наихудшем случае выигрывает 3 ед. = a0 – минимальная цена игры, а для игрока В – и первая и вторая стратегии дают наибольший проигрыш 5 ед. = b0 максимальная цена игры. Так как нижняя и верхняя цена игры не совпадают, то в чистых стратегиях задача не имеет решения.
Найдём решение задачи в смешанных стратегиях. Будем считать, что игрок В первую стратегию использует с вероятностью q и с вероятностью (1-q) применяет вторую стратегию. Тогда
q 1-q
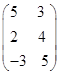
Найдём средний выигрыш игрока А.
Если игрок А выбирает первую стратегию, то получит в среднем
v1=5q+3(1-q)=3+2q
Для второй стратегии игрока А средний выигрыш будет
v2=2q+4(1-q)=4-2q
Для третьей стратегии игрока А средний выигрыш будет
v3=-3q+5(1-q)=5-8q
Так как неизвестной величиной является только одна – вероятность q, то выигрыш игрока А изобразим на графике в переменных (v,q).
Изучим график. Если игрок В зафиксировал вероятность q1, то игрок А имеет возможность выбора стратегии из трёх вариантов: он выберет либо первую стратегию, тогда в среднем будет платить С единиц, либо вторую стратегию, тогда в среднем он будет платить В единиц, либо третью, тогда в среднем он будет платить А единиц. Естественно он заинтересован в наибольшей плате, поэтому он выберет стратегию 1. Понимая это, игрок В захочет заплатить меньше и выберет меньшее q, а именно q0. В результате для различных значений q приходим к верхней огибающей как наилучшем выборе стратегии для игрока А (выделенная жирная линия на рисунке). Тогда наилучший выбор для игрока А – это точка D.
Найдём q0. Так как
 ,
,
то
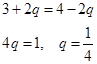
Найдём цену игры.
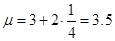
Найдём стратегии игрока А.
Точка D – точка оптимальной стратегии определяется как пересечение второй и третьей стратегий игрока А, поэтому первая и четвёртая стратегии игрока А не используются.
Пусть игрок А с вероятностью p использует стратегию два и с вероятностью (1 – p) – стратегию три. Тогда:
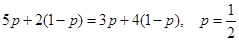
Ответ: игрок А не использует первую и четвёртую стратегии, вторая и третья стратегии используется с равной вероятностью 1/2, игрок В также не использует первую и четвёртую стратегии, вторая стратегия используется с вероятностью ¼, третья стратегия – с вероятностью ¾, при этом цена игры равна 3.5.
Литература
1. Акулич И. Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986.
2. Ашманов С. А. Линейное программирование. – М.: Наука, 1981.
3. Ашманов С. А. Введение в математическую экономику. – М.: Наука, 1984.
4. Банди Б. Методы оптимизации. Вводный курс. – М.: Радио и связь, 1988.
5. Идельсон А. В., Кондратьев В. С.,Заварзина И. А. Методичес-кие указания по курсу “Математическое программирование” для студентов вечернего и заочного факультетов. – Издат.: СПбУЭФ, 1992.
6. Карманов В. Г. Математическое программирование. – М.: Наука, 1986.
7. Ковбаса С. И., Кондратьев В. С., Кондратьева И. В., Савинов Г. В. Методические указания и курсовое задание по курсу “Математическое программирование” для студентов вечерне-заочного факультета. – Издат. СПбУЭФ, 1998.
8.Дмитриев В. Г., Дорошева Е. Н., Савинов Г. Н., Сорокина О. А. Основы линейного программирования – Издат.: СПбГУЭФ, 2006.
9. Шикин Е. В. От игр к играм. Математическое введение. Москва, изд. УРСС, 2003.
 2015-01-07
2015-01-07 899
899








