Решение типовых задач

Задача 1. Из урны, содержащей 3 белых и 7 красных шаров, наудачу последовательно и без возвращения извлекаются два шара. События А ={первый шар белый}, В ={второй шар белый}, С ={по крайней мере один из вынутых шаров белый}. Установить являются ли независимыми А и В, А и С, В и С, события А, В и С в совокупности.

Решение. Так как все необходимые вероятности вычислены в Задаче 1 п. 3.1, то для решения задачи достаточно проверить, выполняется ли для каждой пары событий критерий независимости (1), а для трех событий А, В и С – критерий (2). Имеем

, ,

т.е. события А и В не являются независимыми (в таком случае говорят, что они зависимы). Далее, как установлено в той же задаче,

так как 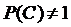. Следовательно, события А и С также зависимы. Наконец, поэтому и события В и С являются зависимыми.

События А, В и С не являются независимыми в совокупности, так как согласно критерию (2) для этого необходимо, чтобы все три события были попарно независимы.

Задача 2. Производятся два последовательных извлечения по одному шару без возвращения из урны, содержащей 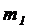белых и черных шаров. События А = {первый шар белый}, В = {второй шар белый}. Показать, что

, (**)

где = {вынутый шар белый} – событие, наблюдаемое в новом эксперименте, состоящем в выборе наудачу одного шара из урны, состав которой изменен в соответствии с условием события А.

Указанный метод вычисления условной вероятности называется методом вспомогательного эксперимента.

Так как эксперимент представляет собой схему выбора без возвращения и с упорядочиванием, то .

.

Аналогично находим

 

Подставляя полученные данные в формулу (*) для вычисления условной вероятности, получаем и первая часть равенства (**) доказана.

Для доказательства второй части равенства (**) заметим, что согласно условию события А один белый шар удален из урны. Новый (вспомогательный) эксперимент состоит в том, что из оставшихся шаров наудачу извлекают один шар. Вероятность, что он окажется белым (событие ), определяется по классической формуле

что и доказывает вторую часть равенства (**).

 

Задачи.

3.11. Пусть А и В – наблюдаемые события в эксперименте, причем Р (А) > 0 и Р (В) > 0 и событие А не зависит от В. Показать, что справедливы следующие утверждения: а) событие В не зависит от А; б) события А и В не зависимы. (Тем самым устанавливается, что свойство независимости двух событий взаимно.)

3.12. Пусть события А и В не совместны, причем и . Доказать, что они зависимы. В частности, отсюда следует, что элементарные исходы любого вероятностного эксперимента зависимы.

3.13. Пусть события А и В независимы и не являются невозможными. Доказать, что они обязательно совместны.

3.14. События А и В зависимы. Следует ли из этого, что они несовместны? Привести пример.

3.15*. Пусть события А и В независимы. Показать, что тогда независимы и события и .

3.16. Пусть для двух наблюдаемых в эксперименте событий А и В выполняются условия А Ω, А Ø, P (A) > 0, P (B / A) = P (B / ). Показать, что события А и В не зависимы.

3.17. Из колоды в 36 карт наудачу извлекается одна карта. События А = {вынутая карта - туз}, В = {вынутая карта черной масти}, F = {вынутая карта – фигура, т.е. является валетом, дамой, королем или тузом}. Установить, зависимы или не зависимы следующие три пары событий А и В, А и F, F и В.

3.18. Подбрасывают наудачу три игральные кости. Установить зависимы или не зависимы события С = {появится не менее двух единиц} и D = {появится четное число нечетных цифр}. Вычислить условную вероятность P (D / C).

3.19. Тетраэдр, три грани которого окрашены в соответственно в красный, желтый и синий цвета, а четвертая грань содержит все три цвета, бросается наудачу на плоскость. События K, G и S состоят в том, что тетраэдр упал на грань, содержащую соответственно красный, желтый либо синий цвет. Доказать, что указанные события попарно независимы, но не являются независимыми в совокупности.

3.20. Из 100 студентов, находящихся в аудитории, 50 человек знают английский язык, 40 – французский и 35 – немецкий. Английский и французский языки знают 20 студентов, английский и немецкий – 8, французский и немецкий – 10. Все три языка знают 5 человек. Один из студентов вышел из аудитории. Рассмотрим следующие события: Е = {вышедший знает английский язык}, F = {вышедший знает французский язык}, D = {вышедший знает немецкий английский язык}.

а) указать все пары независимых событий.

б) установить являются ли события E, F и D независимыми в совокупности.

3.21. Производится два последовательных извлечения по одному шару без возвращения из урны, содержащей белых и черных шаров. События: А = {первый шар белый}, В = {второй шар белый}. Показать, что

,

где = {вынутый шар белый} – событие, наблюдаемое в новом эксперименте, состоящем в выборе наудачу одного шара из урны, состав которой изменен в соответствии с условием события А.

В задачах 3.22. – 3.26. вычислить указанные условные вероятности методом вспомогательного эксперимента.

3.22. Найти вероятность Р (В / А) в условиях эксперимента, описанного в типовой задаче 1.

3.23. В ящике лежат 12 красных, 8 зеленых и 10 синих шаров. Наудачу вынимаются 2 шара. Найти вероятность того, что будут вынуты шары разного цвета, при условии, что не вынут синий шар.

3.24. На шахматную доску наудачу ставятся два слона – белый и черный. Какова вероятность того, что слоны не побьют друг друга, при условии, что белый слон попадет на одно из крайних полей доски?

3.25. Известно, что 5 % всех мужчин и 0,25 % всех женщин – дальтоники. На обследование прибыло одинаковое число мужчин и женщин. Наудачу выбранное лицо оказалось дальтоником. Какова вероятность, что это мужчина?

3.27. На шахматную доску наудачу ставят две ладьи. Вычислить Р (В / А), если А = {ладьи попали на клетки разного цвета}, В = {ладьи побьют друг друга}.

3.28. Доказать, что для любого эксперимента любое наблюдаемое событие А не зависит от события Ω. Объяснить этот результат.