Решение типовых задач

Задача 1. Из полной колоды в 52 карты наудачу последовательно и без возвращения выбирают две карты. Какова вероятность того, что второй картой можно покрыть первую? (Это значит, что вторая картой должна быть более старшей картой той же масти.)

Решение. Пусть А – интересующее нас событие. В качестве первой попытки выберем следующие гипотезы: Н_k = {в составе вынутых карт ровно k картинок}, k = 0, 1, 2 (к картинкам относятся валет, дама, король и туз каждой масти).

Ясно, что { Н_k } (k = 0, 1, 2) – разбиение множества Ω. Нетрудно вычислить безусловные вероятности гипотез Р (Н_k).

Однако вычисление условных вероятностей Р (А / Н_k) оказывается делом не менее трудным, чем ответ на первоначально поставленный вопрос о вероятности события Р (А). Это объясняется тем, что связь события А с данными гипотезами Н_k не может быть достаточно прост описана на языке алгебраических операций.

Рассмотрим более удачный для решения задачи вариант разбиения { Н_k } (k = 2, 3, …, 14), где Н_k = {первая вытянутая карта оценивается в k очков}, при этом значению k = 2 соответствует двойка, k = 3 – тройка, k = 11 – валет, k = 12 – дама, k = 13 – король, k = 14 – туз.

Вычислим условные вероятности, применяя метод вспомогательного эксперимента.

Р (А / Н_k) = Р {вторая вынутая карта той же масти, причем ее достоинство оценивается не ниже, чем в k + 1 очко} = 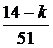в силу формулы классической вероятности. Безусловные вероятности гипотез Р (Н_k) = 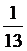в силу равновероятности событий Н_k = {вытянуть карту произвольной масти, оцениваемую в k очков}. Применяя формулу полной вероятности, получим

.

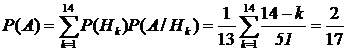Еще более простой путь решения получается, если ввести следующее разбиение множества Ω в данном эксперименте: { Н_k } (k = 1, 2), где Н₁ = {обе вынутые карты одной масти}, Н₂ = {две карты разной масти}. Очевидно, что Р (А / Н₂) = 0, поэтому вторая гипотеза исключается из формулы полной вероятности и Р (Н₁) 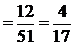(первая карта может быть произвольной масти, вторая должна быть той же масти, что и первая). Пусть теперь выполнено событие Н₁, т.е. обе карты одной масти. Тогда та из них, которую извлекали второй по счету, должна быть старше первой. Но в Силу равновероятности исходов 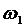= {вторая карта старше первой} и 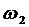= {первая карта старше второй} в этом вспомогательном эксперименте получаем Р (А / Н₁) = 0,5, поэтому

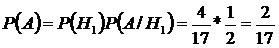
Задача 2. На трех автоматических станках изготавливаются одинаковые детали. Известно, что 30% продукции производится первым станком, 25% - вторым и 45% - третьим. Вероятность изготовления детали, отвечающей стандарту, на первом станке равна 0,99, на втором – 0,988 и на третьем – 0,98. Изготовленные в течении дня на трех станках нерассортированные детали находятся на складе. Определить вероятность того, что наудачу взятая деталь не соответствует стандарту.

Решение. Пусть событие А - наудачу взятая деталь не соответствует стандарту. Гипотезы: 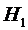- выбранная деталь изготовлена на первом станке; 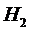- выбранная деталь изготовлена на втором станке и 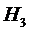- выбранная деталь изготовлена на третьем станке. Из условий задачи легко находятся следующие вероятности для некоторой детали, выбранной случайно из всей дневной продукции:

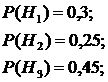
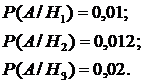
По формуле полной вероятности находим вероятность того, что наудачу взятая деталь не соответствует стандарту:

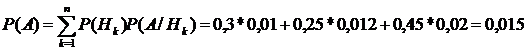
Задачи.

3.29. Прибор, установленный на борту самолета, может работать в двух режимах: в условиях нормального крейсерского полета и в условиях перегрузки при взлете и посадке. Крейсерский режим полета осуществляется в 80% всего времени полета, условия перегрузки в 20%. Вероятность выхода прибора из строя за время полета в нормальном режиме равна 0,1, в условиях перегрузки 0,4. Вычислить надежность прибора за время полета.

3.30. В продажу поступают телевизоры трех заводов. Продукция первого завода содержит 20% телевизоров со скрытым дефектом, второго – 10% и третьего 5%. Какова вероятность приобрести исправный телевизор, если в магазин поступило 30% телевизоров с первого завода, 20% - со второго и 50% - с третьего?

3.31. Два цеха штампуют однотипные детали. Первый цех делает 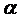% брака, второй - 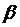%. Для контроля отобрано 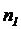деталей из первого цеха и 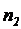из второго. Эти 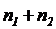смешаны в одну партию, и из нее наудачу извлекают одну деталь. Какова вероятность того, что она бракованная?

3.32. Производится п независимых выстрелов зажигательными снарядами по резервуару с горючим. Каждый снаряд попадает в резервуар с вероятностью р. Если в резервуар попал один снаряд, то горючее воспламеняется с вероятностью р₁, если два снаряда – с полной достоверностью. Найти вероятность того, что при п выстредах горючее воспламенится.

3.33. При переливании крови надо учитывать группу крови донора и больного. Человеку, имеющему четвертую группу крови, можно перелить кровь любой группы; человеку со второй или третьей группой крови можно перелить кровь либо той же группы, либо первой; человеку с первой группой крови можно перелить только кровь первой группы. Среди населения 33,7% имеют первую, 37,5% - вторую, 20,9% - третью и 7,9% - четвертую группу крови. Найти вероятность того, что случайно взятому больному можно перелить кровь случайно взятого донора.

3.34. По каналу связи, состоящему из передатчика, ретранслятора и приемника, передаются два сигнала: единица и нуль. Сигналы передаются с равной вероятностью и вследствие помех могут искажаться. Вычислить вероятность события С = {принято два одинаковых символа}.

3.35. На рис. 3.2 изображена схема дорог. Туристы выходят из пункта П₁, выбирая каждый раз на развилке дорог дальнейший путь наудачу. Какова вероятность, что они попадут в пункт П₂?

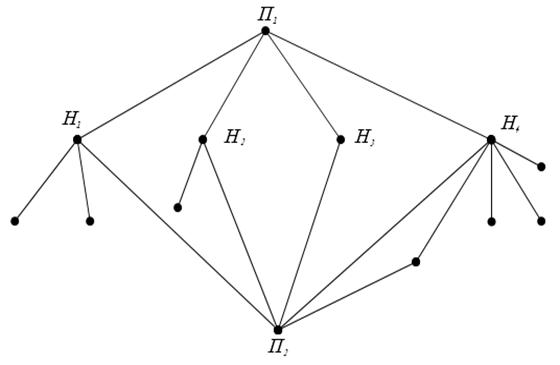
рис. 3.2

3.36. Три стрелка, вероятности попадания которых при одном выстреле в мишень в неизменных условиях постоянны и соответственно равны р₁ = 0,8, р₂ = 0,7, р₃ = 0,6, делают п одному выстрелу в одну и ту же мишень. Вычислить вероятность события А = {в мишени окажется ровно две пробоины}, приняв в качестве гипотез элементарые исходы данного эксперимента.

3.37. В ящике лежат 20 теннисных мячей, в тм числе 15 новых и 5 игранных. Для игры наудачу выбираются два мяча и после игры возвращаются обратно. Затем для второй игры также наудачу извлекаются еще два мяча. Какова вероятность того, что вторая игра будет проводиться новыми мячами?

3.38. Из десяти студентов, пришедших сдавать экзамен по теории вероятностей и взявших билеты, Иванов и Петров знают 20 билетов из 30, Сидоров плохо занимался весь семестр и успел повторить только 15 билетов. По проишествии отведенного времени на подготовку экзаменатор наудачу вызывает отвечать одного из студентов. Какова вероятность того, что вызванный сдал экзамен, если знание билета гарантирует ему сдачу с вероятностью 0,85, а при незнании билета можно сдать экзамен лишь с вероятностью 0,1?

3.39. Шесть шаров, среди которых 3 белых и 3 черных, распределены по двум урнам, Наудачу выбирается урна, а из нее - один шар. Как нужно распределить шары по урнам, чтобы вероятность события А = {вынутый шар белый}была максимальной?

3.40*. Для поиска месторождения нефти на заданной территории организовано п геологоразведочных партий, каждая из которых независимо от других обнаруживает залежь с вероятностью р. После обработки и анализа сейсмографических записей вся территория была поделена на два района. В первом районе нефть может залегать с вероятностью р₁, а во втором - с вероятностью 1 - р₁. Как следует распределить п геологоразведочных партий по двум районам, чтобы вероятность обнаружения нефти была максимальной?

3.41. Программа экзамена содержит 30 различных вопросов, из которых студент Иванов знает только 15. Для успешной сдачи экзамена достаточно ответить на 2 предложенных вопроса или на один из них и на дополнительный вопрос. Какова вероятность того, что Иванов успешно сдаст экзамен?

3.42. Из множества чисел Е = {1, 2, …, n } наудачу последовательно и без возвращения извлекают два числа. Какова вероятность того, что первое число больше второго не менее, чем на m ()?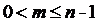

3.43. На шахматную доску ставят на удачу двух слонов, белого и черного. Какова вероятность того, что слоны побьют друг друга?

3.44. Из полного набора домино, содержащего числа 0, 1, 2, …, n наудачу отбирают 2 кости. Какова вероятность, что их можно приставить друг к другу?

3.45*. В урне находятся 7 белых и 3 черных шара. Три игрока по очереди извлекают по одному шару, отмечают цвет и возвращают шар обратно. Выигрывает тот, кто первым достанет черный шар. Найти вероятность выигрыша для каждого из игроков, если игра моет продолжаться неограниченно.

3.46. Студент Иванов знает только 10 из 25 экзаменационных билетов. В каком случае шансы Иванова получить известный ему экзаменационный билет выше: когда он подходит тянуть билет первым или вторым?

3.47. В урну, содержащую п шаров, опущен белый шар, после чего наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).

3.48. В вычислительной лаборатории имебтся шесть клавишных автоматов и четыре полуавтомата. Вероятность того, что за время выполнения некоторого рассчета автомат не выйдет из строя, равна 0,95; для полуавтомата эта вероятность равна 0,8. Студент производит рассчет на наудачу выбранной машине. Найти вероятность того, что до окончания рассчета машина не выйдет из строя.

3.49. В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.

3.50. В ящике содержится 12 деталей, изготовленных на заводе №1, 20 деталей – на заводе №2 и 18 деталей – на заводе №3. Вероятность того, что деталь, изготовленная на заводе №1, отличного качества равна 0,9; для деталей, изготовленных на заводах №2 и №3, эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества.

3.51. В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.

3.52. В каждой из трех урн содержится 6 черных и 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что шар наудачу извлеченный из третьей урны, окажется белым.

3.55. Вероятность того, что во время работы цифровой электронной машины произойдет сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах, относятся как 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.