2017-11-01
585
Произведением вектора на число 
называется вектор 
, модуль которого 
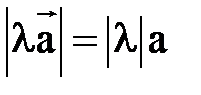, а направление совпадает с направлением вектора 
, либо противоположно ему, смотря по тому λ > 0. либо λ < 0, т. е. 
, 
, 
.
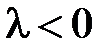Умножение вектора на число обладает свойством ассоциативности, т. е.
и двумя свойствами дистрибутивности:
;
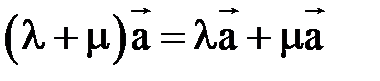Векторы 
называются линейно независимыми, или просто независимыми, если не существует чисел 
, из которых по крайней мере одно отлично от нуля, и 
Упражнение 29. Показать, что
1) два вектора независимы тогда и только тогда, когда они ненулевые и неколлинеарны;
2) три вектора линейно независимы 
они ненулевые и не существует параллельной им плоскости; такие векторы называются некомпланарными;
3) тривектора, лежащие в одной плоскости всегда зависимы;
4) любые четыревектора всегда линейно зависимы.
