Векторным произведением векторов 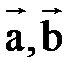 называется вектор
называется вектор 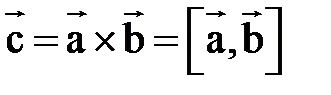 , определяемый следующим образом. В общем случае этот вектор по модулю равен площади параллелограмма, построенного на векторах
, определяемый следующим образом. В общем случае этот вектор по модулю равен площади параллелограмма, построенного на векторах 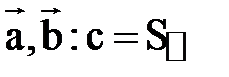 , и направлен перпендикулярно плоскости этого параллелограмма, т.е.
, и направлен перпендикулярно плоскости этого параллелограмма, т.е. 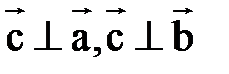 , так что векторы
, так что векторы 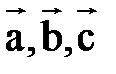 образуют правую тройку.
образуют правую тройку.
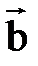
|
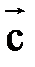
|
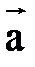
|
В особых случаях, если хотя бы один из векторов 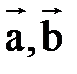 равен нуль-вектору
равен нуль-вектору 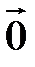 или векторы коллинеарны
или векторы коллинеарны 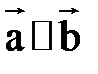 , то
, то 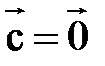 .
.
Свойства векторного произведения:
1) 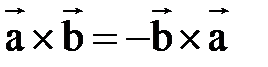
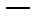 антикоммутативность;
антикоммутативность;
2) 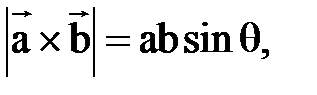
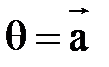 ^
^ 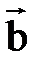 ;
;
3) 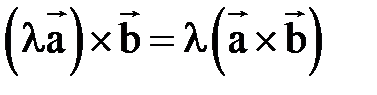 ;
;
4) 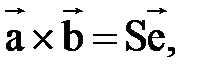
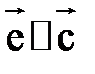 .
.
5) 
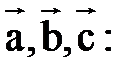
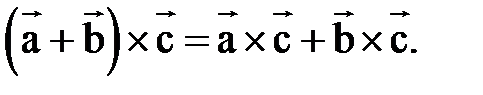
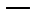 дистрибутивность.
дистрибутивность.
Отметим ещё одно тождество:

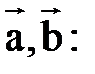
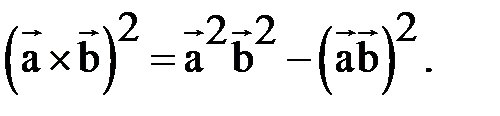 (4)
(4)
Упражнение 30. Показать, что 
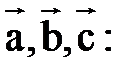
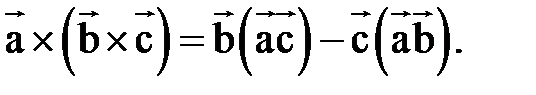
 2017-11-01
2017-11-01 466
466








