2017-11-01
1102
Если диаметр пересекает коническое сечение, то касательная в точке пересечения идёт в направлении, сопряжённом направлению диаметра.
Действительно, пусть 
- точка пересечения диаметра y = kx с эллипсом или гиперболой 
. Уравнение касательной в этой точке 
. Найдём её угловой коэффициент 
:
, 
, 
.
Поскольку точка 
лежит на диаметре, то 
. Поэтому
, что совпадает с формулой (5).
В случае параболы 
уравнение касательной к ней в точке 
имеет вид: 
. Найдём угловой коэффициент 
, 
.
Диаметр, сопряжённый хордам с угловым коэффициентом k, имеет уравнение (7). Если хорды параллельны касательной, то
,
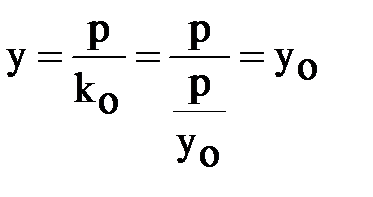т.е. получим диаметр 
, пересекающий параболу в точке 
, что и требуется.
Упражнение 24. Доказать, что любой эллипс можно представить как проекцию окружности из другой плоскости. Показать, что сопряжённым диаметрам эллипса в этом проектировании соответствуют перпендикулярные диаметры окружности. Доказать, что площадь параллелограмма, образованного касательными в концах сопряжённых диаметров, постоянна.
Упражнение 25. Показать, что площадь части плоскости, ограниченной эллипсом с полуосями a, b равна π a b. Заметим, что при a = b получим 
.
Упражнение 26. Можно ли в эллипс вписать треугольник так, чтобы касательная в каждой его вершине была параллельна противоположной стороне? С каким произволом это можно сделать? Чему равна площадь такого треугольника, если полуоси эллипса a, b?
