2017-11-01
608
Углом между векторами 
и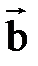 
называется угол 
между векторами 
и 
имеющими общее начало.
Скалярным произведением векторов 
и 
называется число 
, равное произведению их модулей на косинус угла между векторами: 
.
Скалярное произведение обладает следующими очевидными свойствами:
1) 
2) 
; 3)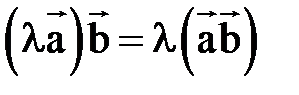 
;
4) если модуль b = 1, то 
;
5) 
когда векторы перпендикулярны или один из векторов равен нуль вектору 
.
Векторной проекцией или просто проекцией вектора 
на прямую называется вектор 
, началом и концом которого служат проекции начала и конца вектора 
.
Очевидно, что равные векторы имеют равные проекции, но не наоборот.
Проекция суммы векторов равна сумме их проекций: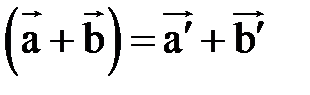 
.
Скалярное произведение векторов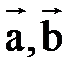 
равно, в частности, скалярному произведению вектора 
на проекцию 
, вектора 
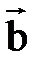на прямую, содержащую вектор 
, т.е. 
. (1)
Если 
некомпланарные векторы, то из трёх равенств
следует 
Действительно, если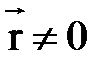 
, то из указанных равенств следует 
, 
, 
, а значит, векторы 
параллельны любой плоскости, перпендикулярной вектору 
, т.е. компланарны, что противоречит условию.
Скалярное произведение обладает свойством дистрибутивности, т. е.
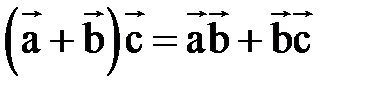. (2)
