Смешанное произведение векторов

Смешанным произведением трёх векторов называется число . (1)

Если один из векторов равен нуль-вектору, то смешанное произведение равно нулю.

Теорема. Смешанное произведение ненулевых векторов , непараллельных одной плоскости, равно по абсолютной величинеобъёму V парллелепипеда, построенного на этих векторах как на сторонах.

Действительно,

(2)

где S - площадь основания, построенного на векторах 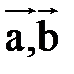, а - единичный вектор, перпендикулярный основанию и образующий с векторами правую тройку.

Подставим выражение векторного произведения (2) в определение(1):

() =

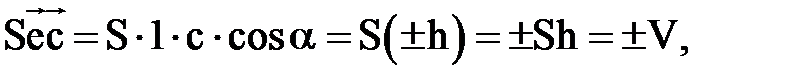
где h – высота параллелепипеда, знак «+» соответствует правой тройке векторов , а левой – знак «-».

Значит, V = ± ().

Теорема.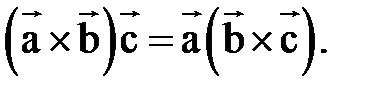

В самом деле, 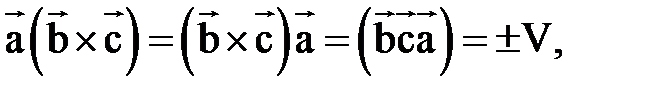т. е. правая и левая части равенства (3) равны по абсолютной величине и по знаку, т. к. 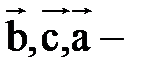правая тройка, точнее, той же ориентации, что и тройка .

Из определения (1) и свойства (3) следует, что при перестановке местами любых двух сомножителей смешанного произведения () оно меняет знак. В частности, если два сомножителя равны, то смешанное произведение равно нулю.

Вообще же, обращение смешанного произведения в нуль означает компланарность векторов .