2017-11-01
443
Пусть 
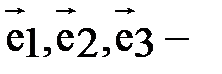три некомпланарных вектора.
Теорема. Любой вектор 
допускает единственное представление
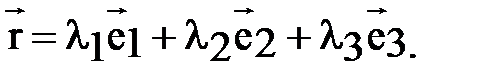(1)
Числа 
называются аффинными координатами вектора 
относительно базиса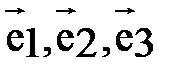 
. Разложение записывают кратко 
.
Выясним геометрический смысл координат вектора, если базис ортонормирован, т. е. состоит из единичных, попарно ортогональных векторов, которые часто обозначают 
. Координаты в этом случае называют декартовыми.
Умножая скалярно равенство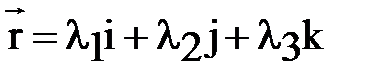 
(1)
последовательно на 
и учитывая единичность длин и ортогональность векторов декартового базиса, получаем 
, 
, 
.
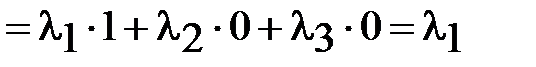Откуда 
, 
, 
, где
, 
, 
.
Полученный результат можно выразить словами: декартовы координаты вектора 
суть скалярные проекции этого вектора на оси, определяемые базисными векторами.
Пусть , 
. Тогда
,
,
.
Следовательно, у коллинеарных векторов координаты пропорциональны.
Найдём скалярное произведение векторов и 
в декартовом базисе
.
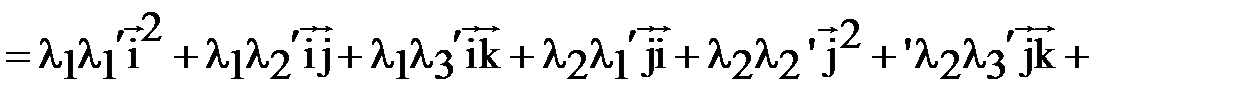
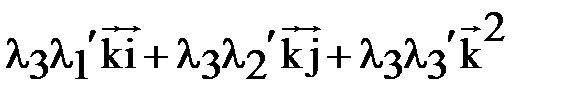Получим
.
Рассмотрим смешанное произведение векторов декартового базиса: 
. Правой тройке соответствует знак «+», а левой - «-».
|
|
|
Допустим, как обычно, что тройка векторов - правая. Перемножим векторно векторы правого декартового базиса:
, 
.
С помощью этих соотношений найдём векторное произведение в декартовых координатах:
= 
=
= 
=
= 
.
Эти координаты получаются при разложении следующего определителя по первой строке
.
Найдём, наконец, смешанное произведение векторов 
, 
, 
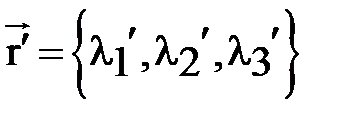в декартовых координатах:
,
откуда
.
