Простейшие задачи в пространстве

Проведём из произвольной точки О пространства три прямые 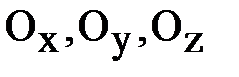, не лежащие в одной плоскости, и отложим на прямых от точки О ненулевые векторы 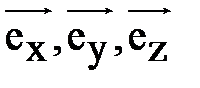. Согласно § 6 главы 4 любой вектор допускает единственное представление: .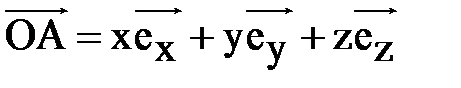

Числа x, y, z называют аффинными координатами точки А, а вектор 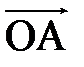- её радиус вектором.

Если прямые 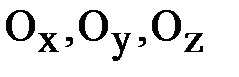перпендикулярны друг другу, а векторы единичны, т.е. , , 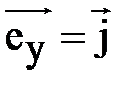, 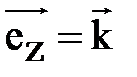то получаем обычные декартовы координаты точки A (x, y, z), которыми пользуются чаще.

Пусть в пространстве введена аффинная система координат .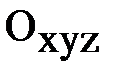

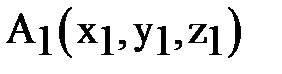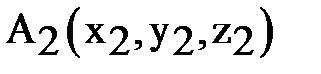, - две произвольные точки пространства. Найдём координаты точки А, делящей направленный отрезок в отношении .

В этом случае выполняется равенство 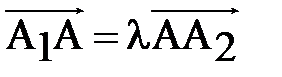, из которого находятся координаты точки A (x, y, z)

, , .

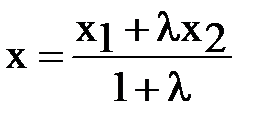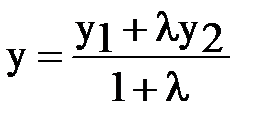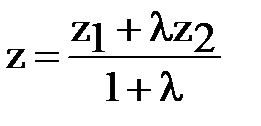Пусть теперь система координат , как обычно, декартова. Выразим расстояние d между точками через координаты этих точек. Расстояние d равно модулю вектора и вычисляется по формуле

.

Выразим площадь треугольника плоскости xy через координаты его вершин 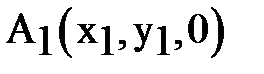, , 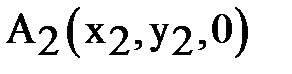. Модуль вектора равен удвоенной площади . Так как

, ,

,

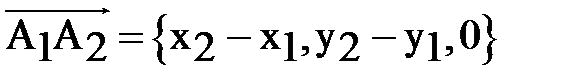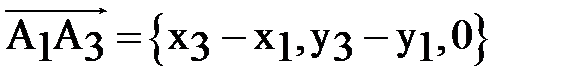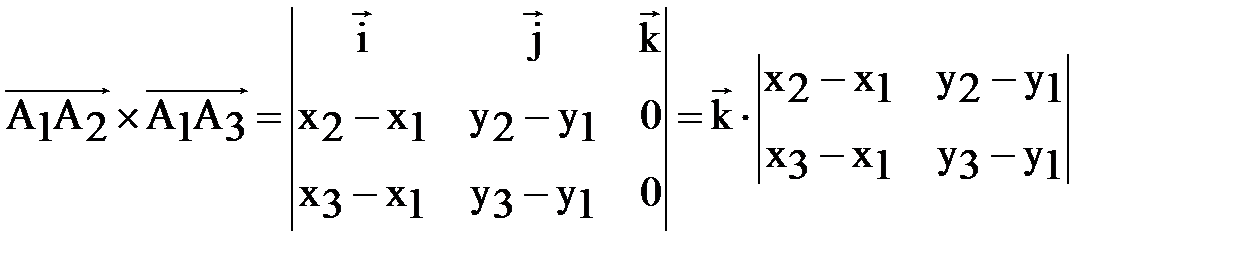То площадь треугольника

.

Выразим объём тетраэдра через координаты его вершин

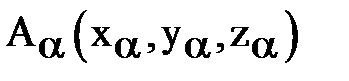, где 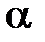= 1, 2, 3, 4. Смешанное произведение векторов

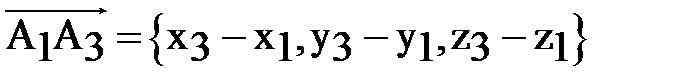, , с точностью до знака равно объёму параллелепипеда 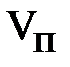, построенному на этих векторах:

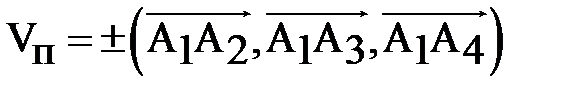. Отсюда

.

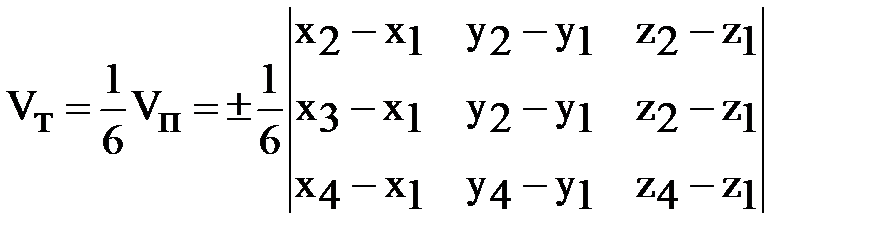Упражнение 31. Доказать, что прямые, соединяющие середины противоположных рёбер тетраэдра, пересекаются в одной точке. Выразить её координаты через координаты вершин тетраэдра.

Упражнение 32. Доказать, что прямые, соединяющие вершины тетраэдра с центрами тяжести противоположных граней, пересекаются в одной точке. Выразить её координаты через координаты вершин тетраэдра.