2017-11-01
910
Пусть в пространстве введены две аффинные системы координат 
и 
. Выразим координаты произвольной точки А в системе координат через её координаты в системе .
Имеем:
, 
,
. (1)
Векторы 
однозначно представляются через векторы 
:
(2)
где 
- координаты вектора 
относительно базиса 
. Формулы (2) можно записать короче: 
.
Подставим формулы (2) в выражение (1):
+ + 
+ 
= = 
+ 
+ + 
.
Выражения в скобках этой формулы суть координаты вектора 
относительно базиса , т.е. координаты x, y, z точки А в системе .
Получили: 
Причем выполняется условие
Формулы (3) дают переход от координат точки в системе к координатам в системе . Однако, если их подставить в уравнение поверхности 
, то получим уравнение этой поверхности в виде 
относительно системы с началом 
.
Если обе системы координат и 
декартовы, то коэффициенты 
формул (3) удовлетворяют условиям
, 
, 
.
Эти условия получаются с помощью формул (2) и соотношений для базисов
, 
, 
, 
=0 
.
В случае декартовых координат базисы часто обозначают 
и 
. Находим: 
, 
, где знаки не согласованы. Если знаки одинаковы, то одну систему координат можно движением совместить с другой. В этом случае базисы имеют одинаковую ориентацию. Если знаки различны, то совмещение возможно движением и зеркальным отражением, т.е. базисы разной ориентации.
Упражнение 36. Показать, что переход от одной декартовой системы координат к другой Оxyz с тем же началом О можно выполнить в 3 этапа:
Углы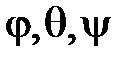 
называются углами Эйлера. Выяснить их геометрический смысл.
