Уравнение 
 (1)
(1)
называется уравнением поверхности в неявной форме, если координаты каждой точки поверхности удовлетворяют этому уравнению. И обратно, любая тройка чисел (x, y, z), удовлетворяющая уравнению, представляет собой координаты одной из точек поверхности. Неявные уравнения поверхности часто встречаются в аналитической геометрии.
Если уравнение (1) удаётся разрешить относительно одной из переменных, например, выразить
z = f (x, y), (2)
то получаем явное уравнение поверхности.
Систему уравнений 
 ,
,  , (3)
, (3)
задающих координаты точек как функции 2-х параметров u, v, называют уравнениями поверхности в параметрической форме. Это наиболее общий способ задания поверхности, которым пользуются в дифференциальной геометрии.
Исключая параметры u, v из системы (3), можно получить уравнение поверхности в явном виде. Явное уравнение (2) всегда можно тривиальным образом представить неявно f (x,y) – z = 0 и в параметрическом виде: x = u, y = v, z = f (u,v).
Пример 1. Рассмотрим круговой цилиндр с осью Oz и радиусом R. Возьмём в качестве параметров u, v, характеризующих положение точки (x, y, z) на цилиндре, угол, который плоскость, проходящая через ось Oz и точку (x, y, z), образует с плоскостью xz, и аппликату z точки (x, y, z).
 |
 |
 |
 |
 |
 |
 |
 |
Тогда получим уравнения цилиндра в параметрической форме:
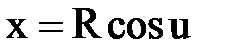 ,
,  ,
,  .
.
В плоскости xy первые два уравнения есть параметрические уравнения окружности – направляющей цилиндра. Возведём их обе части в квадрат и сложим почленно:
 .
.
Получили неявное уравнение окружности в плоскости x y:
 .
.
Это же уравнение в пространстве является неявным уравнением цилиндра. Отсутствие координаты z в нём означает, что она не связана с координатами x, y. Аппликата z может быть любой.
Систему уравнений  ,
, 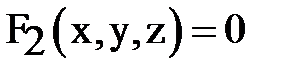 (4)
(4)
называют неявными уравнениями кривой. Каждое уравнение системы (4) есть неявное уравнение поверхности, поэтому здесь кривая есть линия пересечения 2-х поверхностей.
Систему уравнений  ,
,  ,
,  , (5)
, (5)
задающую координаты точек кривой как функции некоторого параметра t, называют параметрическими уравнениями кривой.
В физике t – время, поэтому линия представляется как след движущейся точки.
Если система (4) разрешается относительно 2-х координат, например,
 ,
,  , то она приводится к специальному параметрическому виду:
, то она приводится к специальному параметрическому виду:
 ,
, 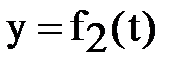 , z = t. (6)
, z = t. (6)
Наоборот, если из системы  можно выразить параметр
можно выразить параметр  , например
, например  , то подставив его в остальные уравнения
, то подставив его в остальные уравнения
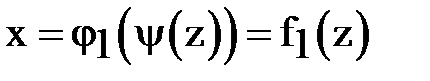 ,
, 
получим систему уравнений кривой в специальном явном виде. Это два некруговых цилиндра с осями  , Ox, которые пересекаются по линии.
, Ox, которые пересекаются по линии.
Пример 2. Рассмотрим окружность в пространстве. Любую окружность можно представить как пересечение двух сфер. Следовательно, окружность может быть задана системой уравнений:
 ,
,
 ,
,
причём их центры  ,
,  и радиусы
и радиусы  должны удовлетворять некоторым ограничениям, обеспечивающим пересечение сфер. Если разности возвести в квадраты и вычесть одно уравнение из другого, то получим линейное уравнение плоскости, в которой лежит окружность. Окружность можно представить как сечение любой из 2-х сфер этой плоскостью.
должны удовлетворять некоторым ограничениям, обеспечивающим пересечение сфер. Если разности возвести в квадраты и вычесть одно уравнение из другого, то получим линейное уравнение плоскости, в которой лежит окружность. Окружность можно представить как сечение любой из 2-х сфер этой плоскостью.
Кривая и поверхность могут не пересекаться, пересекаться в отдельных точках, либо лежать одна на другой. Если поверхность задаётся уравнением (1), а кривая – двумя уравнениями (4), то точки пересечения удовлетворяют системе уравнений (1), (4). Решая эту систему, находим координаты точек пересечения, если они есть.
Упражнение 33. Окружность задана пересечением двух сфер:
 ,
,
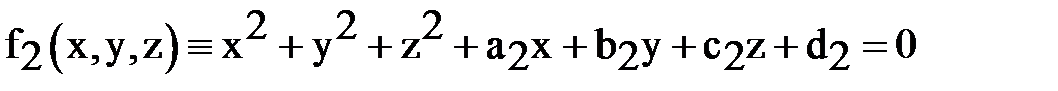 .
.
Найти ограничения на коэффициенты. Показать, что уравнение любой сферы, проходящей через эту окружность, можно задать уравнением
 .
.
Упражнение 34. Составить уравнение прямого кругового конуса с осью Oz, вершиной О и углом  при вершине.
при вершине.
Упражнение 35. Показать, что кривая  при вращении около оси z описывает поверхность, задаваемую уравнением
при вращении около оси z описывает поверхность, задаваемую уравнением  .
.
 2017-11-01
2017-11-01 3103
3103
