Эллипсоид
Каноническое уравнение эллипсоида имеет вид. Исследование этого уравнения позволяет построить поверхность следующей формы.
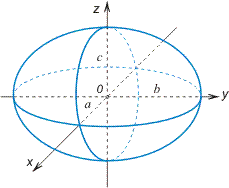
Положительные числа 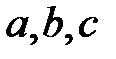 называются полуосями эллипсоида и представляют собой длины отрезков, отсекаемых на осях координат эллипсоидом. Точки пересечения осей с эллипсоидом (1) называются вершинами эллипсоида. У эллипсоида 6 вершин. Из уравнения (1) видно, что координатные плоскости являются плоскостями симметрии эллипсоида, а начало координат – центром симметрии.
называются полуосями эллипсоида и представляют собой длины отрезков, отсекаемых на осях координат эллипсоидом. Точки пересечения осей с эллипсоидом (1) называются вершинами эллипсоида. У эллипсоида 6 вершин. Из уравнения (1) видно, что координатные плоскости являются плоскостями симметрии эллипсоида, а начало координат – центром симметрии.
Подобно тому, как эллипс получается равномерным сжатием из окружности, эллипсоид получается сжатием из сферы относительно двух перпендикулярных плоскостей. Если 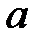 - большая полуось эллипсоида, то он может быть получен из сферы
- большая полуось эллипсоида, то он может быть получен из сферы 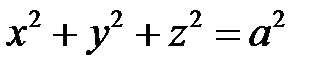 , уравнение которой запишем в виде
, уравнение которой запишем в виде
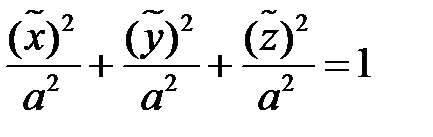 .
.
Сожмем эту сферу относительно плоскости 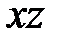 с коэффициентом
с коэффициентом 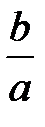 и относительно плоскости
и относительно плоскости 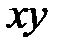 с коэффициентом
с коэффициентом 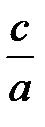 . Координаты
. Координаты 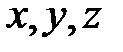 точек сжатой поверхности выражаются через координаты
точек сжатой поверхности выражаются через координаты 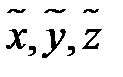 точек сферы по формулам
точек сферы по формулам 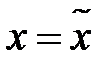 ,
, 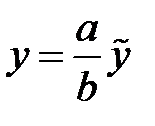 ,
, 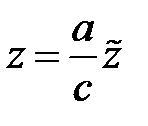 . Найдем
. Найдем 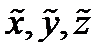 и подставим их в уравнение (2):
и подставим их в уравнение (2):
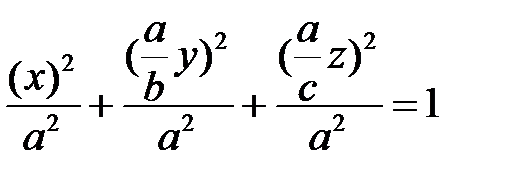 .
.
Возведем в квадраты и сократим на 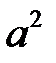 , получим уравнение (1).
, получим уравнение (1).
Если две полуоси эллипсоида равны, например, 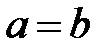 , то он называется эллипсоидом вращения:
, то он называется эллипсоидом вращения:
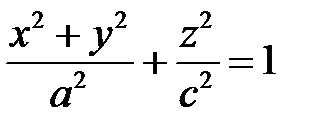 .
.
Действительно, пересечем его плоскостью 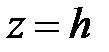 , параллельной плоскости
, параллельной плоскости 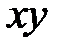 :
: 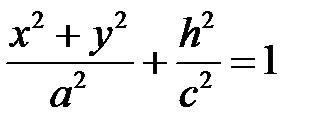 ,
, 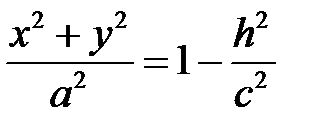 , тогда
, тогда 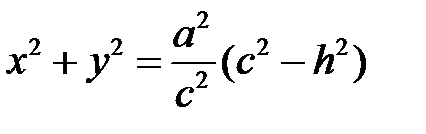 . Если
. Если 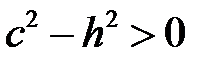 ,
, 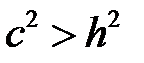 ,
, 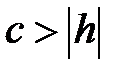 ,
, 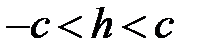 , то получаем окружность в плоскости
, то получаем окружность в плоскости  с центром на оси
с центром на оси 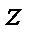 и радиусом
и радиусом 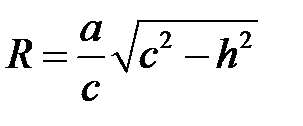 . Таким образом, этот эллипсоид образуется при вращении эллипса
. Таким образом, этот эллипсоид образуется при вращении эллипса 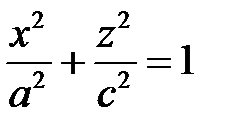 , лежащего в плоскости
, лежащего в плоскости 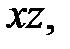 или эллипса
или эллипса 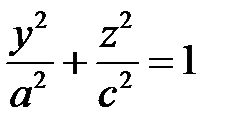 из плоскости
из плоскости 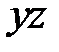 около оси
около оси 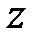 . Если все три полуоси эллипсоида равны, то он является сферой.
. Если все три полуоси эллипсоида равны, то он является сферой.
Упражнение 49. Доказать, что линия пересечения эллипсоида с плоскостью является эллипсом. Найти фокусы эллипса.
Упражнение 50. Показать, что эллипсоид вращения 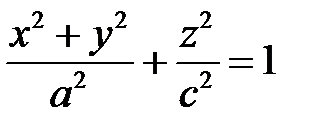 при
при  есть геометрическое место точек, сумма расстояний от которых до двух данных точек, называемых фокусами, постоянна. Найти фокусы эллипсоида вращения. Дать определение эллипсоида вращения как геометрического места точек, если
есть геометрическое место точек, сумма расстояний от которых до двух данных точек, называемых фокусами, постоянна. Найти фокусы эллипсоида вращения. Дать определение эллипсоида вращения как геометрического места точек, если  .
.
Упражнение 51. Пусть имеем эллипсоид 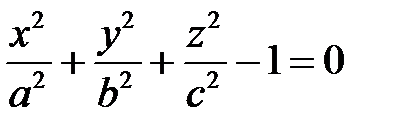 . Показать, что если поверхность
. Показать, что если поверхность 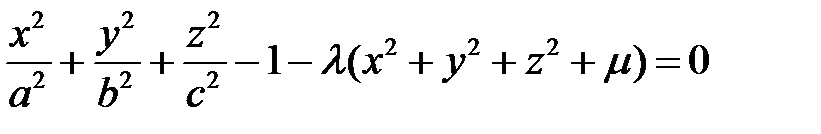 распадается на пару плоскостей, то эти плоскости пересекают эллипсоид по окружностям. Обосновать на этом способ разыскания круговых сечений эллипсоида.
распадается на пару плоскостей, то эти плоскости пересекают эллипсоид по окружностям. Обосновать на этом способ разыскания круговых сечений эллипсоида.
Упражнение 52. Показать, что эллипсоид 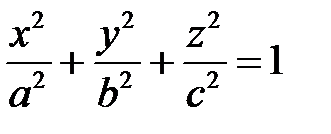 допускает задание параметрическими уравнениями
допускает задание параметрическими уравнениями 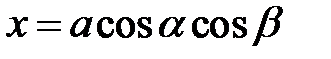 ,
, 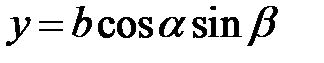 ,
, 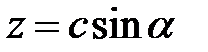 . Найти области изменения параметров
. Найти области изменения параметров 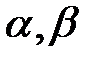 .
.
Упражнение 53. Найти уравнение кривой на плоскости 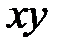 , ограничивающей область, в которую эллипсоид
, ограничивающей область, в которую эллипсоид 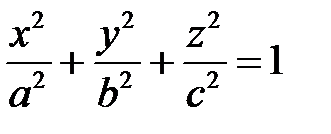 проектируется прямыми, параллельными прямой
проектируется прямыми, параллельными прямой 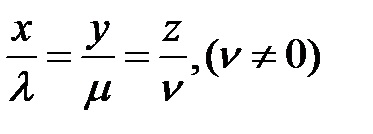 . Записать уравнения линии, лежащей на эллипсоиде, которая проектируется в эту кривую. Является ли линия на эллипсоиде плоской кривой?
. Записать уравнения линии, лежащей на эллипсоиде, которая проектируется в эту кривую. Является ли линия на эллипсоиде плоской кривой?
Гиперболоиды
Канонические уравнения гиперболоидов имеют вид:
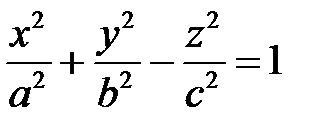 ,
,
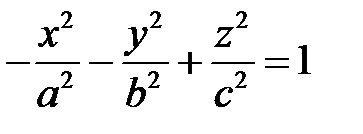 .
.
Поверхность с уравнением (1), в котором один минус, называется однополостным гиперболоидом, а с уравнением (2), в котором два минуса, - двуполостным гиперболоидом. Однополостной и двуполостной гиперболоиды выглядят следующим образом:
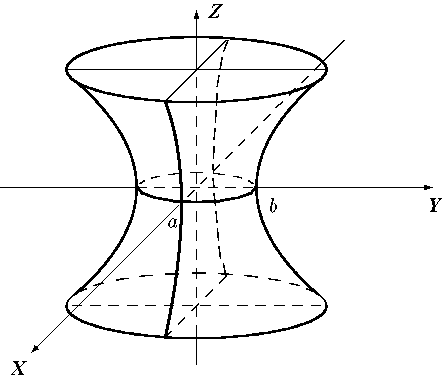
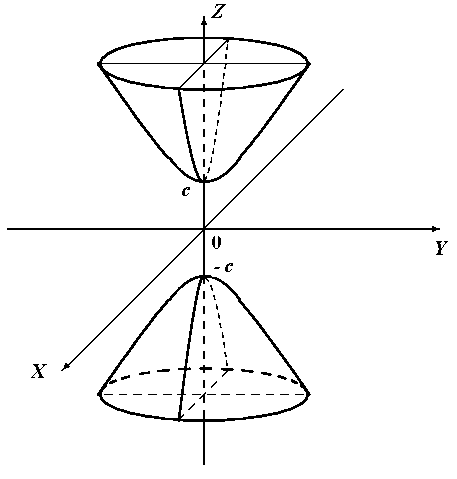
Оба гиперболоида имеют координатные плоскости плоскостями симметрии, а начало координат – центром симметрии.
Если действительные полуоси 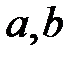 однополостного гиперболоида равны, то он имеет уравнение
однополостного гиперболоида равны, то он имеет уравнение 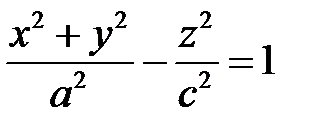 , называется гиперболоидом вращения и получается вращением около оси
, называется гиперболоидом вращения и получается вращением около оси 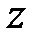 гиперболы
гиперболы 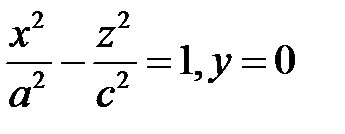 или гиперболы
или гиперболы 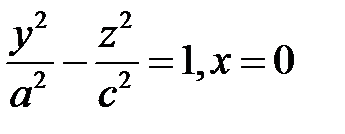 . Ось
. Ось 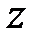 является мнимой осью этих гипербол.
является мнимой осью этих гипербол.
Если мнимые полуоси 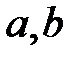 двуполостного гиперболоида равны, то он имеет уравнение
двуполостного гиперболоида равны, то он имеет уравнение 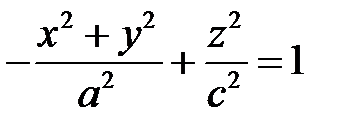 , называется гиперболоидом вращения и получается вращением вокруг оси
, называется гиперболоидом вращения и получается вращением вокруг оси 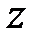 гиперболы
гиперболы 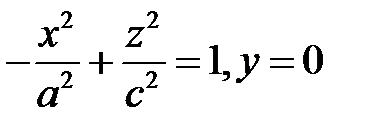 или гиперболы
или гиперболы 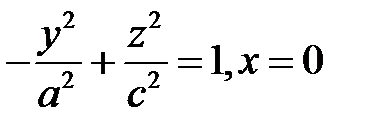 . Ось
. Ось 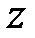 является действительной осью этих гипербол. Общие гиперболоиды, у которых
является действительной осью этих гипербол. Общие гиперболоиды, у которых 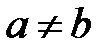 , могут быть получены из соответствующих гиперболоидов вращения равномерным сжатием, либо растяжением относительно плоскости
, могут быть получены из соответствующих гиперболоидов вращения равномерным сжатием, либо растяжением относительно плоскости 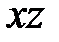 в отношении
в отношении 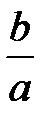 .
.
При пересечении гиперболоидов произвольной плоскостью могут получится различные конические сечения. Например, сечение однополостного гиперболоида (1) горизонтальной плоскостью 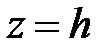 дает
дает 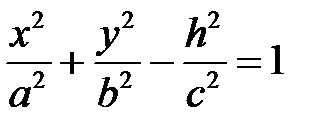 ,
, 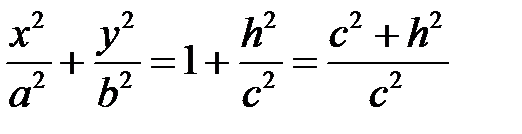 , тогда
, тогда 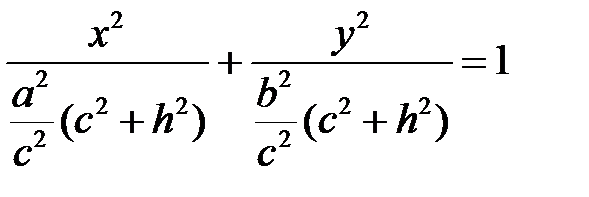 или
или 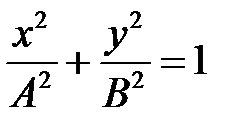 , где
, где 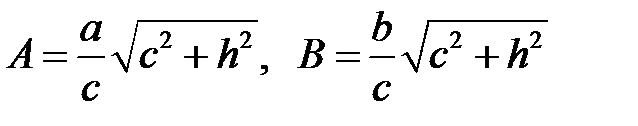 . Это эллипс, расположенный в плоскости
. Это эллипс, расположенный в плоскости 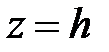 , с полуосями
, с полуосями 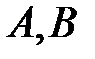 .
.
Плоскость 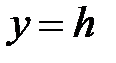 , параллельная плоскости
, параллельная плоскости 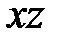 , пересекает гиперболоид (1) следующим образом:
, пересекает гиперболоид (1) следующим образом: 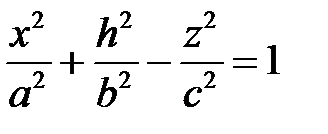 , тогда
, тогда
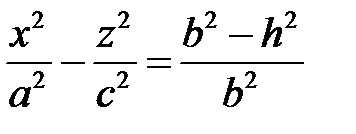 .
.
При 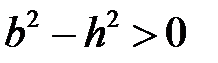 ,
, 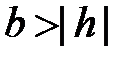 ,
, 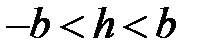 , уравнение (3) преобразуется так:
, уравнение (3) преобразуется так: 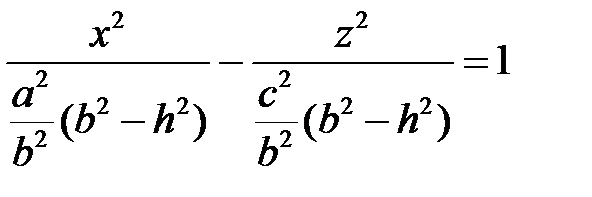 , или
, или 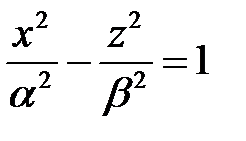 , где
, где 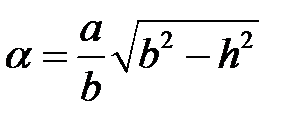 ,
, 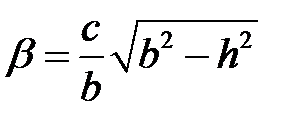 . Это гипербола, расположенная в плоскости
. Это гипербола, расположенная в плоскости 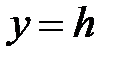 , с действительной осью, параллельной оси
, с действительной осью, параллельной оси 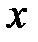 .
.
Если 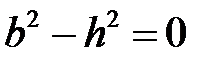 ,
, 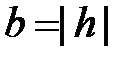 ,
, 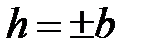 , то уравнение (3) упрощается:
, то уравнение (3) упрощается: 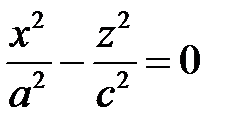 ,
, 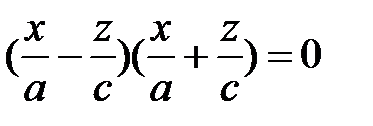 , тогда
, тогда 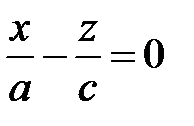 или
или 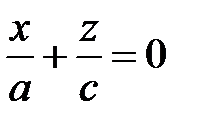 , т.е.
, т.е. 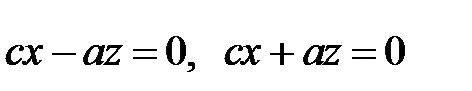 .
.
Это уравнения прямых в плоскости 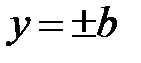 , пересекающих ось
, пересекающих ось 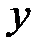 и лежащих на однополостном гиперболоиде. Они называются прямолинейными образующими.
и лежащих на однополостном гиперболоиде. Они называются прямолинейными образующими.
При 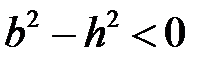 ,
, 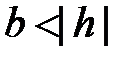 , тогда
, тогда 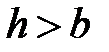 или
или 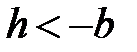 , умножим уравнение (3) на
, умножим уравнение (3) на 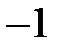 :
: 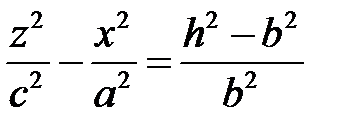 ,
, 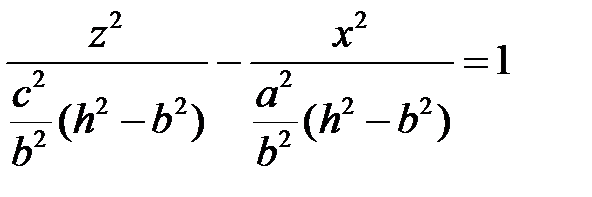 или
или 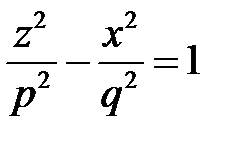 , где
, где 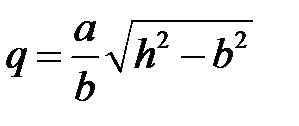 ,
, 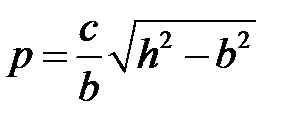 . Это гипербола в плоскости
. Это гипербола в плоскости 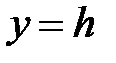 с действительной осью, параллельной
с действительной осью, параллельной 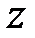 .
.
Упражнение 54. Составить уравнение однополостного гиперболоида, который образуется при вращении прямой 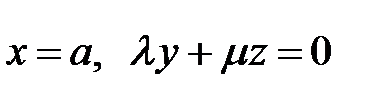 около оси
около оси 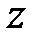 .
.
Упражнение 55. Найти круговые сечения однополостного гиперболоида. Существуют ли круговые сечения двуполостного гиперболоида?
Упражнение 56. Показать, что через каждую точку пространства, не принадлежащую координатным плоскостям, проходят три поверхности семейства с параметром 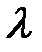
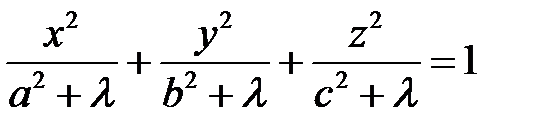 - эллипсоид, однополостной и двуполостной гиперболоиды.
- эллипсоид, однополостной и двуполостной гиперболоиды.
Параболоиды
Канонические уравнения параболоидов имеют вид:
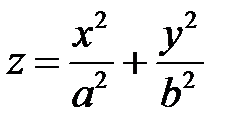 ,
,
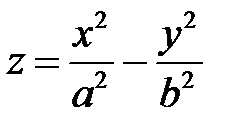 .
.
Параболоид с уравнением (1), содержащим левую часть уравнения эллипса, называется эллиптическим параболоидом. Параболоид с уравнением (2), включающим левую часть уравнения гиперболы, называется гиперболическим параболоидом.
Эллиптический и гиперболический параболоиды выглядят следующим образом:
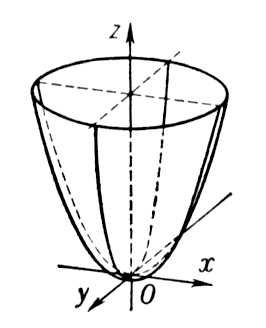
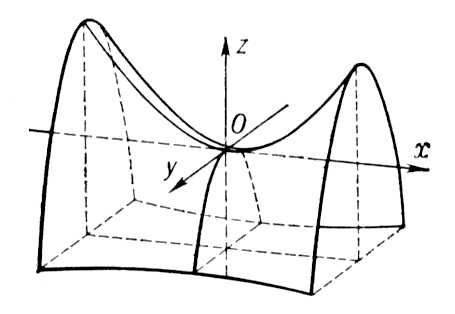
Плоскости 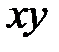 и
и 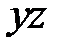 являются плоскостями симметрии параболоидов. Ось
являются плоскостями симметрии параболоидов. Ось 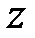 называется осью параболоида, а пересечение оси с поверхностями (1) и (2) – вершиной параболоида.
называется осью параболоида, а пересечение оси с поверхностями (1) и (2) – вершиной параболоида.
При 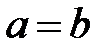 эллиптический параболоид (1) называется параболоидом вращения. Он имеет уравнение
эллиптический параболоид (1) называется параболоидом вращения. Он имеет уравнение
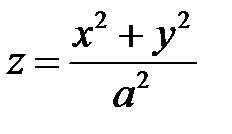
и получается при вращении параболы 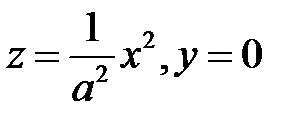 или параболы
или параболы 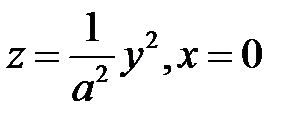 около оси
около оси 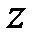 . Общий эллиптический параболоид
. Общий эллиптический параболоид 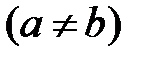 можно получить из параболы вращения (3) равномерной деформацией, т.е. сжатием, либо растяжением с коэффициентом
можно получить из параболы вращения (3) равномерной деформацией, т.е. сжатием, либо растяжением с коэффициентом 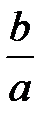 относительно плоскости
относительно плоскости 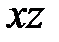 .
.
Параболоиды пересекаются плоскостями, параллельными координатным плоскостям 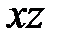 и
и 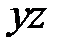 , по равным, параллельно расположенным параболам.
, по равным, параллельно расположенным параболам.
Действительно, например, плоскость 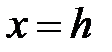 пересекает эллиптический параболоид (1) по линии
пересекает эллиптический параболоид (1) по линии 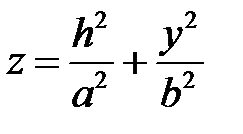 . В плоскости
. В плоскости 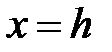 это уравнение параболы
это уравнение параболы 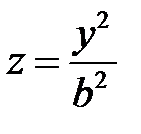 , сдвинутой на
, сдвинутой на 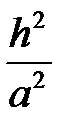 в положительной направлении оси
в положительной направлении оси 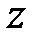 . Следовательно, эллиптический параболоид (1) образуется при параллельном сдвиге параболы
. Следовательно, эллиптический параболоид (1) образуется при параллельном сдвиге параболы 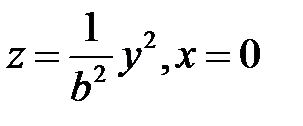 , когда ее вершина движется вдоль параболы
, когда ее вершина движется вдоль параболы 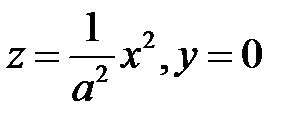 . Аналогично образуется гиперболический параболоид.
. Аналогично образуется гиперболический параболоид.
Горизонтальная плоскость 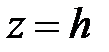 пересекает эллиптический параболоид следующим образом. Подставим уравнение плоскости в уравнение (1):
пересекает эллиптический параболоид следующим образом. Подставим уравнение плоскости в уравнение (1):
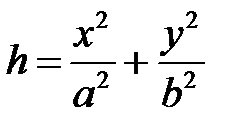
При 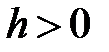 имеем
имеем 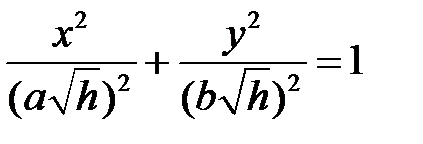 - эллипс в плоскости
- эллипс в плоскости 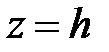 .
.
Если  , то уравнение (4) упрощается:
, то уравнение (4) упрощается: 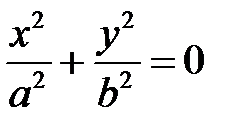 . Это уравнение точки
. Это уравнение точки 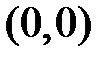 в координатной плоскости
в координатной плоскости 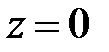 .
.
При 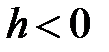 уравнение (4) не имеет решений, т.е. плоскость
уравнение (4) не имеет решений, т.е. плоскость 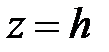 не пересекается с эллиптическим параболоидом.
не пересекается с эллиптическим параболоидом.
Гиперболический параболоид (2) всегда пересекается горизонтальной плоскостью 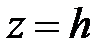 . В самом деле, имеем
. В самом деле, имеем
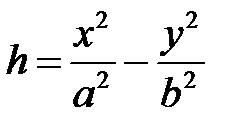
При 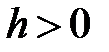 ,
, 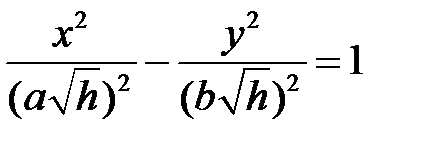 - уравнение гиперболы в плоскости
- уравнение гиперболы в плоскости 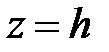 с действительной осью, параллельной оси
с действительной осью, параллельной оси 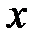 .
.
Если  , то уравнение (5) упрощается:
, то уравнение (5) упрощается: 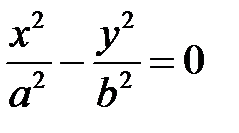 ,
, 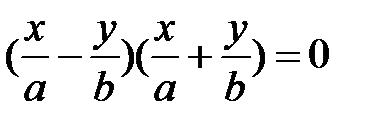 , тогда
, тогда 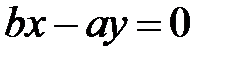 или
или 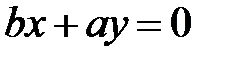 - две прямые в плоскости
- две прямые в плоскости 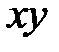 , пересекающиеся в начале координат и являющиеся прямолинейными образующимися гиперболического параболоида.
, пересекающиеся в начале координат и являющиеся прямолинейными образующимися гиперболического параболоида.
При 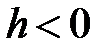 умножим уравнение (5) на
умножим уравнение (5) на 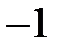 :
: 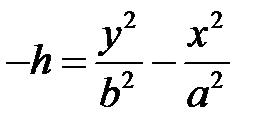 , получим
, получим 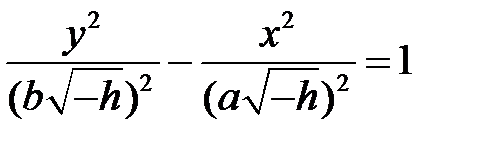 - уравнение гиперболы в плоскости
- уравнение гиперболы в плоскости 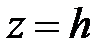 с действительной осью, параллельной оси
с действительной осью, параллельной оси 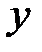 .
.
Упражнение 57. Показать, что эллиптический параболоид вращения есть геометрическое место точек, равноудаленных от некоторой плоскости, называемой директориальной, и точки – фокуса. Найти фокус и директориальную плоскость парабол оида 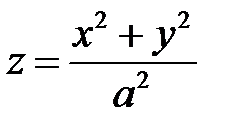 .
.
Упражнение 58. Показать, что никакая плоскость не пересекает эллиптический параболоид по гиперболам.
Конусы и цилиндры
Канонические уравнения конусов и цилиндров имеют следующий вид:
1. Конус
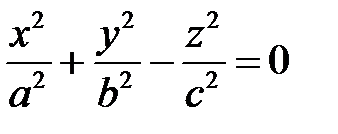 .
.
2. Эллиптический цилиндр
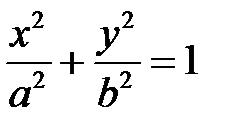 .
.
3. Гиперболический цилиндр
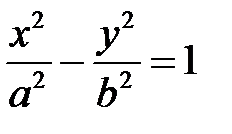 .
.
4. Параболический цилиндр
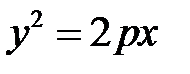 .
.
Эти поверхности имеют такую форму:
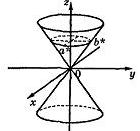
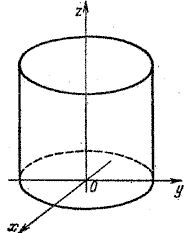
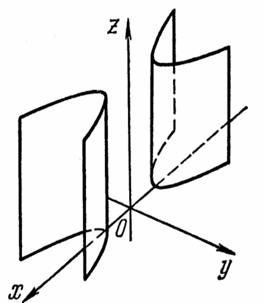
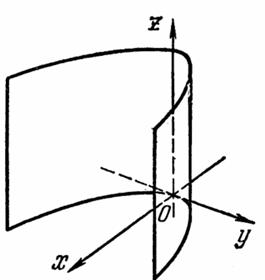
Эллиптический, гиперболический и параболический цилиндры пересекают плоскость 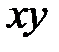 по эллипсу, гиперболе и параболе соответственно. Они образуются прямыми, параллельными оси
по эллипсу, гиперболе и параболе соответственно. Они образуются прямыми, параллельными оси 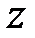 и пересекающими данные кривые.
и пересекающими данные кривые.
Общий конус (1) получается из кругового конуса 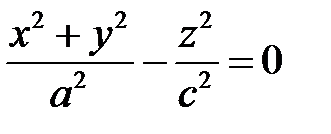 равномерной деформацией относительно плоскости
равномерной деформацией относительно плоскости 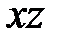 . Общий эллиптический цилиндр (2) получается деформацией из кругового цилиндра
. Общий эллиптический цилиндр (2) получается деформацией из кругового цилиндра 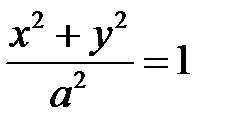 .
.
С однополостным гиперболоидом
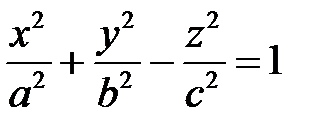
и двуполостным гиперболоидом
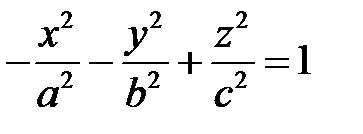
естественным образом связан конус (1), который называется асимптотическим конусом. Сделаем рисунок:
Каждая плоскость, проходящая через ось 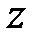 , пересекает гиперболоиды по сопряженным гиперболам, а конус – по двум образующим, которые являются асимптотами этих
, пересекает гиперболоиды по сопряженным гиперболам, а конус – по двум образующим, которые являются асимптотами этих 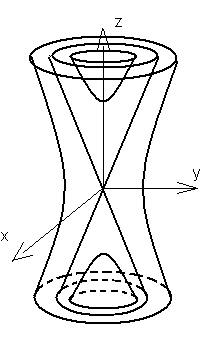 гипербол. В частности, плоскость
гипербол. В частности, плоскость 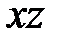 с уравнением
с уравнением 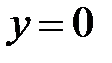 пересекает гиперболоид (5) по гиперболе
пересекает гиперболоид (5) по гиперболе
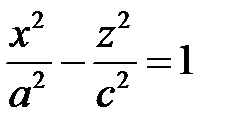
с действительной осью 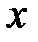 , а гиперболоид (6) по гиперболе
, а гиперболоид (6) по гиперболе
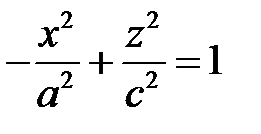
с действительной осью 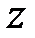 . Конус (1) пересекается этой плоскостью по двум прямым
. Конус (1) пересекается этой плоскостью по двум прямым 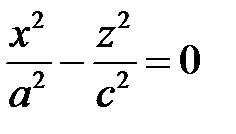 ,
, 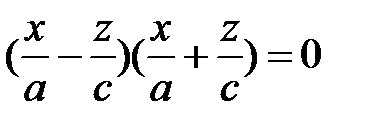
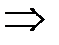
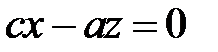 ,
, 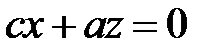 . Они являются асимптотами сопряженных гипербол (7) и (8).
. Они являются асимптотами сопряженных гипербол (7) и (8).
Упражнение 59. Показать, что уравнение кругового конуса с вершиной в начале координат, осью 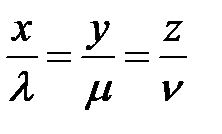 и углом при вершине
и углом при вершине 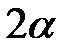 можно записать в виде
можно записать в виде
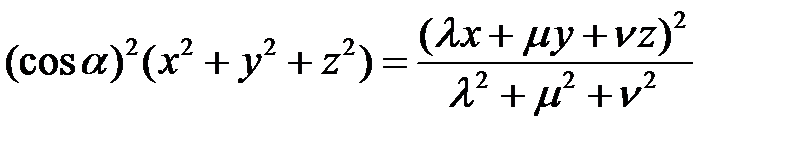 .
.
Упражнение 60. Показать, что уравнение кругового цилиндра с осью 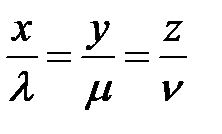 и радиуса
и радиуса 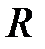 можно записать в виде
можно записать в виде
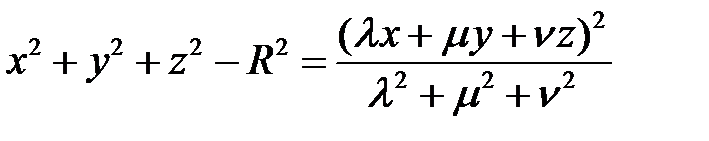 .
.
Практикум
| Тема практического занятия | Номера задач для аудиторной работы | Номера задач для домашней работы |
| Тема 1. Векторы | ||
| 1.1. Равенство векторов. Линейные операции над векторами (сложение и умножение на число) | [4]: №№1002, 1021, 1022 | [4]: №№1013, 1026, 1017, 1018, 1025 |
| 1.2. Проекции векторов. Скалярное произведение векторов; угол между двумя векторами. Векторное и смешанное произведение векторов. | [4]: №№1029, 1031, 1034, 1038, 1043, 1046 | [4]: №№1040, 1049, 1052, 1053, 1054 |
| 1.3. Коллинеарные и компланарные векторы; координаты вектора относительно данного базиса | [4]: 1019, 1022, 1023, 1026 | [4]: №№1075, 1076, 1079, 1080 |
| Тема 2. Системы координат на плоскости и в пространстве | ||
| 2.1. Расстояние между двумя точками и углы между векторами в аффинной, декартовой и полярной системах координат | [4]: №№41, 42, 44, 46, 54, 91, 94, 109 | [4]: №№43, 51, 52, 53, 55, 93, 95, 110 |
| 2.2. Формулы перехода от одной системы координат к другой | [4]: №№126, 128, 131, 136, 137 | [4]: №№ 127, 129, 130, 132 |
| 2.3. Нахождение объема ориентированного параллелепипеда | [4]: №№1083, 1084(1), 1085, 1086(1) | [4]: 1084(2), 1086(2, 3) |
| Тема 3. Прямая линия на плоскости | ||
| 3.1. Способы задания прямой линии на плоскости | [4]: №№185(1), 196(1, 3), 197(1, 2, 3), 198, 200*, 203* | [4]: №№185(2, 3), 196(2, 4), 197(4), 198, 201* |
| 3.2. Исследование взаимного расположения двух прямых на плоскости. Вычисление угла между двумя прямыми на плоскости | [4]: №№271(1, 3), 272, 281, 291*, 294, 296(1, 3), 297, 299, 300(1, 3), 301* | [4]: №№271(2, 4), 288, 290, 293*, 296(2, 4), 298, 300(2, 4), 305 |
| Тема 4. Кривые второго порядка | ||
| 4.1. Исследование свойств эллипса, гиперболы и параболы по их каноническим уравнениям | [4]: №№346, 375, 376, 326, 333, 334 | [4]: №№337, 338, 341, 401, 433, 479, 480, 434, 498 |
| 4.2. Параметрическая запись уравнения эллипса; построение эллипса по точкам. Эллипс как результат сжатия окружности к одному из ее диаметров, как проекция окружности и как сечение круглого цилиндра | [4]: №№424, 427 | [4]: №№425, 429 |
| 4.3. Нахождение асимптот гиперболы, директрис и фокального параметра эллипса и гиперболы | [4]: №№439, 439*, 440, 441, 470 | [4]: №№439, 452, 449, 469 |
| Тема 5. Общая теория кривых второго порядка | ||
| 5.1. Пересечение кривой второго порядка с прямой. Асимптотические направления кривых второго порядка. Нахождение уравнения касательной | [4]: №№564, 565, 567(1, 3), 568, 572, 571, 573 | [4]: №№575, 574, 566, 567(2, 4), 570 |
| 5.2. Центр кривой второго порядка | [4]: №№540(1, 3, 5), 542(1, 3), 544(1), 546 | [4]: №№540(2, 4, 6, 7, 8), 542(2, 4), 544(2, 3) |
| 5.3. Диаметры кривой второго порядка. Сопряженные направления. Асимптоты. | [4]: №№589, 594(1,3) 596, 597, 598, 625(1) | [4]: №№590, 594(2), 599, 600, 601, 605, 608, 625(2, 3, 4) |
| 5.4. Нахождение главных направлений и главных диаметров кривой второго порядка | [4]: №№609(1,2), 611, 612(1) | [4]: №№609(3), 612(2, 3) |
| 5.5. Приведение уравнения кривой второго порядка к каноническому виду | [4]: №№618(1.3), 620(1), 622, 623(1, 3) | [4]: №№618(2, 4, 5), 620(2), 623(2) |
| 5.6. Исследование кривых второго порядка при помощи инвариантов | [4]: №№549, 552, 553, 638(1, 3), 639(1, 3), 642(1) | [4]: №№638(2, 4, 5), 639(2, 4), 641, 642(2) |
| Тема 6. Плоскость и прямая в пространстве | ||
| 6.1. Уравнения плоскости в пространстве | [4]: №№753, 757(1), 758(1, 3), 764, 770, 771(1) | [4]: №№757(2, 3), 758(2, 4), 761, 771(2, 3), 773 |
| 6.2. Способы задания прямой в пространстве | [4]: №№817, 820(2), 821, 822(1), 848 | [4]: №№818, 820(1, 3), 822(2), 825 |
| 6.3. Взаимное расположение прямых и плоскостей в пространстве. Угол между прямой и плоскостью; угол между двумя плоскостями | [4]: №№847, 775, 781, 831, 836, | [4]: №№838, 850, 851, 859 |
| Тема 7. Поверхности второго порядка | ||
| 7.1. Распадающиеся поверхности | [4]: №№946(3) | Задача: выяснить, какие из перечисленных поверхностей распадаются |
| 7.2. Цилиндрические и конические поверхности | [4]: №№876, 878, 880, 881, 882, 884 | [4]: №№877, 879, 883, 885 |
| 7.3. Исследование свойств эллипсоидов, гиперболоидов и параболоидов по их каноническим уравнениям | [4]: №№890, 892, 894, 896, 899(1) | [4]: №№891, 893, 895, 897, 899(2, 3) |
| 7.4. Прямолинейные образующие | Задача: по уравнению гиперболоида найти все его прямолинейные образующие. | Задача: по уравнению параболоида найти все его прямолинейные образующие |
| Тема 8. Общая теория поверхностей второго порядка | ||
| 8.1. Пересечение поверхности второго порядка с прямой и с плоскостью. | [4]: №№894, 904(1) | [4]: №№892, 897, 904(2, 3, 4), 905 |
| 8.2. Асимптотические направления. Касательные прямые и касательная плоскость. Особые точки поверхности второго порядка | [4]: №№910, 923, 921 | [4]: №№912, 913, |
| 8.3. Асимптотические направления, конус асимптотических направлений | [4]: №№956(1, 3, 5), 961, 959, 960, 963, 964(1) | [4]: №№956(2, 4), 957, 961, 962, 964(2, 3) |
| 8.4. Центр поверхности второго порядка | [4]: №№941(1, 3, 5), 942, 943(1) | [4]: №№941(2, 4, 6), 943(2, 3) |
| 8.5. Диаметральные плоскости. Особые направления | [4]: №№980(1, 3), 981, 983, 986 | [4]: №№980(2, 4), 982, 984, 988 |
| 8.6. Нахождение главных направлений и главных диаметров кривой второго порядка | [4]: №№989, 991 | [4]: №№990 |
| 8.7. Приведение к каноническому виду уравнения поверхности второго порядка | [2]: №№991, 992, 993(1) | [2]: №№939, 993(5), 994, 995, 996, 997, |
| 8.8. Исследование поверхностей второго порядка при помощи инвариантов | [2]: №№943(1) | [2]: №№941(6), 998 |
 2017-11-01
2017-11-01 6640
6640
