- Уравнение произвольной плоскости, проходящей через точку
 , или связки плоскостей.
, или связки плоскостей.
Любая плоскость задается уравнением
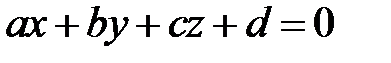 .
.
Так как точка  принадлежит плоскости, то выполняется тождество
принадлежит плоскости, то выполняется тождество  .
.
Вычитаем его из уравнения (1):
 .
.
Получили уравнение плоскости, проходящей через данную точку. Действительно, при любых коэффициентах  уравнение (2) удовлетворяется координатами
уравнение (2) удовлетворяется координатами  .
.
- Уравнения прямой, проходящей через точку
 , или связки прямых.
, или связки прямых.
Искомые уравнения имеют вид 
 .
.
В самом деле, уравнения (3) задают прямую, проходящую через точку  . Давая коэффициентам
. Давая коэффициентам  произвольные значения, не все равные нулю, получаем прямую любого направления, проходящую через заданную точку.
произвольные значения, не все равные нулю, получаем прямую любого направления, проходящую через заданную точку.
3. Уравнения прямой, проходящей через две точки  и
и  .
.
Уравнения прямой можно записать в форме (3). Поскольку вторая точка лежит на прямой, справедливы тождества:
 .
.
Разделив уравнения (3) на эти тождества почленно, исключим параметры 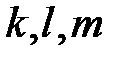 . Получаем уравнения прямой, проходящей через две точки:
. Получаем уравнения прямой, проходящей через две точки:
 .
.
- Уравнение плоскости, проходящей через три точки
 ,
,  и
и  .
.
Пусть  - произвольная точка искомой плоскости. Три вектора
- произвольная точка искомой плоскости. Три вектора  ,
,  и
и  лежат в одной плоскости, т.е. компланарны. Следовательно, их смешанное произведение равно нулю. Записывая его в координатах, получим уравнение плоскости, проходящей через три точки:
лежат в одной плоскости, т.е. компланарны. Следовательно, их смешанное произведение равно нулю. Записывая его в координатах, получим уравнение плоскости, проходящей через три точки:
 .
.
- Уравнение плоскости, проходящей через точку
 параллельно плоскости (1).
параллельно плоскости (1).
Искомое уравнение (2). Эта плоскость проходит через данную точку и параллельна заданной плоскости.
- Уравнения прямой, проходящей через точку
 , параллельно прямой
, параллельно прямой
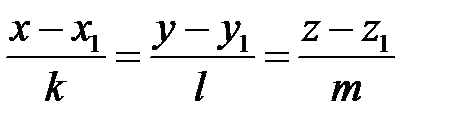 .
.
Искомые уравнения (3).
- Прямая, проходящая через точку
 перпендикулярно плоскости (1)
перпендикулярно плоскости (1)
задается уравнениями  .
.
- Плоскость, проходящая через точку
 перпендикулярно прямой (4)
перпендикулярно прямой (4)
определяется уравнением  .
.
- Уравнение плоскости, проходящей через точку
 параллельно прямым
параллельно прямым  и
и 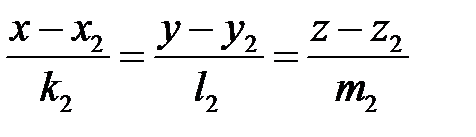 .
.
Пусть  - произвольная точка плоскости, тогда вектор
- произвольная точка плоскости, тогда вектор  лежит в плоскости. Так как векторы
лежит в плоскости. Так как векторы  и
и  параллельны плоскости, то три вектора
параллельны плоскости, то три вектора  ,
,  и
и 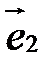 компланарны. Их смешанное произведение равно нулю. В координатах получаем уравнение плоскости, проходящей через данную точку, параллельно двум заданным прямым:
компланарны. Их смешанное произведение равно нулю. В координатах получаем уравнение плоскости, проходящей через данную точку, параллельно двум заданным прямым:
 .
.
Упражнение 45. Показать, что любая плоскость, кроме одной, проходящая через прямую  , задается уравнением вида
, задается уравнением вида  .
.
Упражнение 46. Показать, что коническая поверхность, образованная прямыми, проходящими через начало координат и пресекающими кривую  , задается уравнением
, задается уравнением  .
.
Упражнение 47. Показать, что цилиндрическая поверхность, образованная прямыми, параллельными прямой 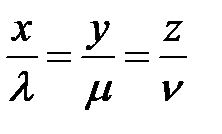 (
( ) и пересекающими кривую
) и пересекающими кривую  плоскости
плоскости  , задается уравнением
, задается уравнением 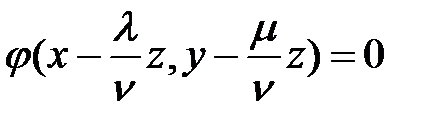 .
.
Упражнение 48. Показать, что поверхность, образуемая при вращении кривой 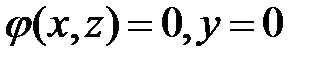 около оси
около оси  , задается уравнением
, задается уравнением  .
.
 2017-11-01
2017-11-01 877
877








