Уравнения прямой в пространстве

Любую прямую можно задать как пересечение двух плоскостей. Следовательно, прямую можно определить системой уравнений:

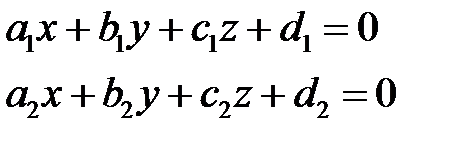
Обратно, любая совместная система двух независимых уравнений (1) представляет собой уравнения некоторой прямой.

Пусть - фиксированная точка прямой, - произвольная точка прямой и - ненулевой вектор, параллельный прямой. Тогда векторы и параллельны, следовательно, их координаты пропорциональны:

Эти, по существу, два уравнения, называют каноническими уравнениями прямой.

Пусть прямая задана уравнениями (1). Составим её уравнения в канонической форме. Для этого достаточно найти какую-нибудь точку на прямой и вектор , параллельный прямой. Всякий вектор , параллельный прямой, будет параллелен каждой из плоскостей системы (1), а значит, перпендикулярен их нормальным векторам и . Имеем: , , тогда, в качестве можно взять, например, их векторное произведение

.

Замечание 1: Канонические уравнения (2), как и уравнения прямой (1) в виде пересечения двух плоскостей, определяются неоднозначно для данной прямой.

От канонических уравнений прямой (2) можно прийти к её уравнениям в параметрической форме. Обозначим

.

Избавимся от знаменателей и перенесем свободные члены вправо:

.

Это самые удобные параметрические уравнения прямой.

Выясним особенности расположения прямой, если некоторые из коэффициентов в канонических или параметрических уравнениях равны нулю. Так как вектор параллелен прямой, то при прямая параллельна плоскости . Аналогично, при прямая параллельна плоскости , при - плоскости . Если и , то прямая параллельна оси z, пр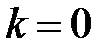и и - оси y, при и - оси х.

Замечание 2: Уравнениями (1), (2) и (4) прямая задается не только в декартовой, но и в аффинной системе координат.

Упражнение 39. Показать, что геометрическое место точек, равноудаленных от трех попарно непараллельных плоскостей, есть прямая.

Упражнение 40. Показать, что геометрическое место точек, равноудаленных от вершин треугольника, есть прямая. Составить её уравнение, если заданы координаты вершин треугольника в пространстве.

Упражнение 41. Показать, что через каждую точку поверхности проходят две прямые, целиком лежащие на поверхности.