2017-11-01
717
Пусть имеем прямую и плоскость, заданные уравнениями:
,
.
Так как вектор 
параллелен прямой, а вектор 
перпендикулярен плоскости, то прямая и плоскость будут параллельны, если эти векторы перпендикулярны: 
,
.
Если при этом координаты точки 
, принадлежащей прямой, удовлетворяют уравнению плоскости 
, то прямая лежит в плоскости.
Прямая и плоскость перпендикулярны, если векторы 
и 
параллельны: 
.
Можно получить условия параллельности и перпендикулярности прямой и плоскости, если прямая задана пересечением двух плоскостей, т.е. системой:
.
Векторы 
и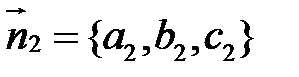 
перпендикулярны соответствующим плоскостям, а вектор 
параллелен линии их пересечения. Имеем: 
,
следовательно, 
, 
, 
. Теперь достаточно воспользоваться условиями (1) и (2).
Пусть две прямые заданы уравнениями в канонической форме:
Поскольку вектор 
параллелен первой прямой, а вектор 
- второй прямой, то прямые параллельны, если 
, т.е. 
. В частности, прямые совпадают, если при этом координаты точки одной прямой, например, 
удовлетворяют уравнениям другой прямой:
.
Прямые перпендикулярны, если векторы 
и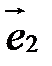 
перпендикулярны: 
, 
.
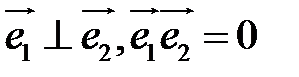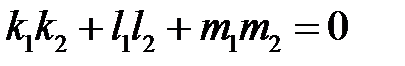Если две прямые заданы уравнениями (3), то легко найти угол между ними вне зависимости от того, пересекаются они, либо скрещиваются. Достаточно найти угол между векторами 
и 
, параллельными прямым. Для одного из двух углов 
между прямыми получаем:
.
Упражнение 42. Найти расстояние между двумя прямыми, заданными уравнениями (3) в канонической форме.
Упражнение 43. Найти уравнение конической поверхности с вершиной , образующие которой пересекают плоскость 
под углом 
.
Упражнение 44. Составить уравнение конической поверхности с вершиной в точке 
, если она проходит через окружность, задаваемую пересечением сферы 
с плоскостью 
. Что представляет собой пересечение этой конической поверхности с плоскостью 
?
