Контрольная работа для заочного отделения
Семестр
Вопросы
- Матрицы. Операции над матрицами. Определения квадратной, нулевой, ступенчатой матрицы. Приведение матрицы к ступенчатому виду. Обратная матрица. Алгоритм вычисления обратной матрицы.
- Определители второго и третьего порядка. Свойства определителей. Способы нахождения (вычисления) определителей 1-го, 2-го,3-го и 4-го порядков. Миноры и алгебраические дополнения элементов. Вычисления определителя разложением его по строке, столбцу.
- Системы линейных уравнений. Система двух уравнений первой степени с двумя неизвестными. Однородная система двух уравнений первой степени с тремя неизвестными. Способы нахождения решений СЛУ. (Матричный метод, метод Гаусса, метод Крамера). Теорема Кронекера-Капелли. Ранг матрицы.
- Векторы. Обозначения векторов. Линейные операции над векторами. Линейная зависимость и линейная независимость векторов. Ортонормированный базис. Скалярное, векторное и смешанное произведение векторов, их свойства.
- Аналитическая геометрия на плоскости. Уравнения линии и прямой. Общее уравнение прямой на плоскости. Уравнение прямой с угловым коэффициентом. Каноническое уравнение прямой на плоскости. Параметрическое уравнение прямой на плоскости.
- Кривые второго порядка. (Эллипс, окружность, гипербола, парабола). Уравнения и графики.
- Плоскость и прямая в пространстве. Уравнение плоскости. Исследование общего уравнения плоскости. Условия параллельности и перпендикулярности плоскостей. Каноническое уравнение прямой в пространстве.
8. Параметрическое задание линии. Примеры линий, заданных параметрически.
9. Уравнение поверхности в пространстве. Цилиндрические поверхности. Сфера. Конусы. Эллипсоид. Гиперболоиды. Параболоиды. Геометрические свойства этих поверхностей,
Рекомендуемая литература
- Клетеник, Д.В. Сборник задач по аналитической геометрии. [Электронный ресурс]: учеб. пособие — Электрон. дан. — СПб.: Лань, 2016. — 224 с. — Режим доступа: http://e.lanbook.com/book/72582
- Владимирский, Б.М. Математика. Общий курс. [Электронный ресурс]: учеб. / Б.М. Владимирский, А.Б. Горстко, Я.М. Ерусалимский. — Электрон. дан. — СПб.: Лань, 2008. — 960 с. — Режим доступа: http://e.lanbook.com/book/634
- Беклемишев, Д.В. Курс аналитеческой геометрии и линейной алгебры. [Электронный ресурс]: учеб. — Электрон. дан. — М.: Физматлит, 2009. — 312 с. — Режим доступа: http://e.lanbook.com/book/2109
- Кадомцев, С.Б. Аналитическая геометрия и линейная алгебра. [Электронный ресурс]: учеб. пособие — Электрон. дан. — М.: Физматлит, 2011. — 168 с. — Режим доступа: http://e.lanbook.com/book/2187
- Аналитическая геометрия и линейная алгебра. Учебное пособие (1.07 Мб)
http://mvt.zb-susu.ru/index.php?view=materials
Пример оформления титульного листа
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
«Южно-Уральский государственный университет»
(национальный исследовательский университет)
Филиал ФГБОУ ВПО «ЮУрГУ» (НИУ) в г. Златоусте
Кафедра «Математика и вычислительная техника»
Контрольная работа
По дисциплине:”математика”
Вариант № 100
Выполнил студент 1 курса
Заочного отделения
Гр…..-166
Иванов И.И.
Проверил………….
Златоуст
201 г.
Введение.
Выполнять контрольную работу следует строго по графику. Каждый студент выполняет контрольную работу под вариантом, номер которого совпадает с его порядковым номером в групповом журнале. Решение задач нужно предоставить в письменном виде на отдельных листах (формата А 4, в скрепленном виде). Сдавать работу можно как в печатном, так и в письменном виде. Выполняя к.р., студент должен переписать условие соответствующей задачи, написать подробное решение, выделив ответ. Там, где это необходимо, дать краткие пояснения по ходу решения.
Задача 1.
Для данного определителя найти миноры и алгебраические дополнения элементов  .Где i и j, определяются следующим образом: для четного варианта i=2, j=4, для нечетного i=1, j=3 Вычислить определитель:
.Где i и j, определяются следующим образом: для четного варианта i=2, j=4, для нечетного i=1, j=3 Вычислить определитель:
а) разложив его по элементам j-й строки
б)получив предварительно нули в i-й строке
1. 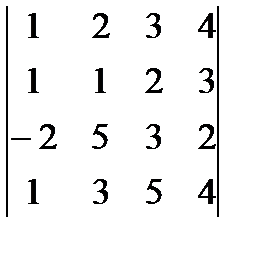 2.
2.  3.
3. 
4.  5.
5.  6.
6. 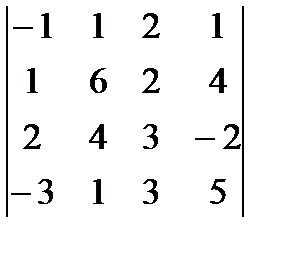
7.  8.
8.  9.
9. 
10.  11.
11.  12.
12. 
13.  14.
14.  15.
15. 
Задача 2.
Проверить совместность системы и в случае совместности решить её:
а)методом Крамера
б)матричным методом
в)методом Гаусса
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 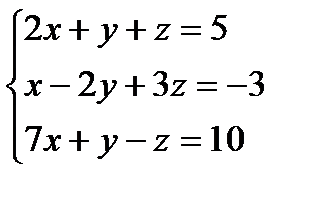
10. 
11. 
12. 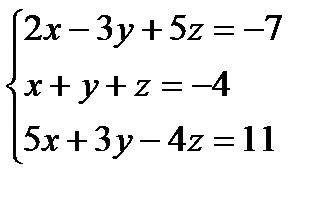
13. 
14. 
15. 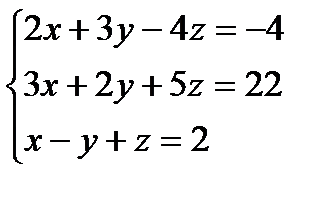
Задача 3.
Решить матричное уравнение
1.  2.
2. 
3.  4
4 
5.  6.
6. 
7. 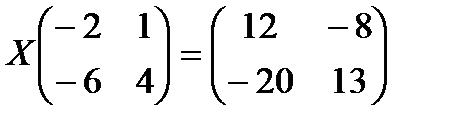 8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15. 
Задача 4.
Выясните, образуют ли векторы  базис. Если образуют, то разложите вектор
базис. Если образуют, то разложите вектор  по этому базису.
по этому базису.
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6.  .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
11.  .
.
12.  .
.
13. 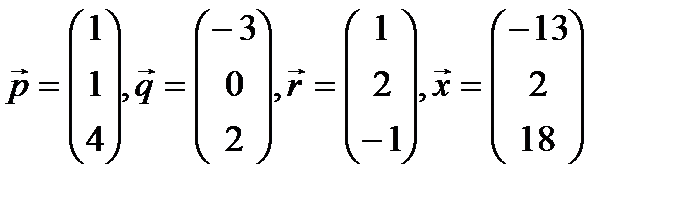 .
.
14.  .
.
15.  .
.
Задача 5.
Заданы вершины треугольника АВС. Вычислите его площадь и косинус внутреннего угла В.
1. 
2. 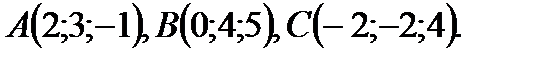
3. 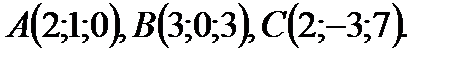
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
Задача 6.
1. Найдите объем параллелепипеда, построенного на векторах  , если
, если 
- Проверьте, лежат ли точки
 в одной плоскости.
в одной плоскости. - Найдите объем параллелепипеда, построенного на векторах

- Найдите объем тетраэдра, построенного на векторах

- Вычислите объем тетраэдра с вершинами в точках

- Найдите объем параллелепипеда, построенного на векторах
 , если
, если 
- Проверьте, лежат ли точки
 в одной плоскости.
в одной плоскости. - Найдите объем параллелепипеда, построенного на векторах

- Найдите объем треугольной пирамиды с вершинами в точках

- При каком значении к точки лежат в одной плоскости

- Найдите объем тетраэдра с вершинами в точках

- При каком значении m векторы
 компланарны?
компланарны? - Проверьте, лежат ли точки
 в одной плоскости.
в одной плоскости. - При каком значении m векторы
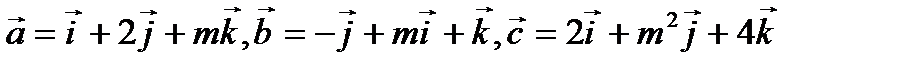 компланарны?
компланарны? - Вычислите объем тетраэдра с вершинами в точках

Задача 7.
В треугольнике АВС составьте уравнения:
1) стороны ВС;
2) высоты, опущенной из вершины А на сторону ВС;
3) медианы, проведенной из вершины С.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 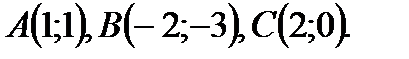
13. 
14. 
15. 
Задача 8.
Напишите каноническое уравнение прямой, проходящей через точку А и перпендикулярной плоскости α.
1. 
2. 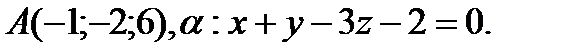
3. 
4. 
5. 
6. 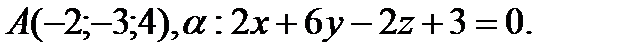
7. 
8. 
9. 
10. 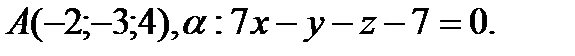
11. 
12. 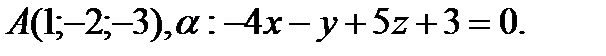
13. 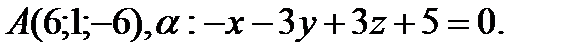
14. 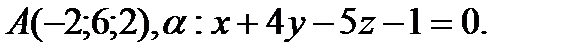
15. 
Задача 9.
Нарисуйте область, ограниченную заданными поверхностями.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
Пример выполнения контрольной работы.
1.Дан определитель четвертого порядка. 
а) Вычислить, разложив его по элементам 1-й строки
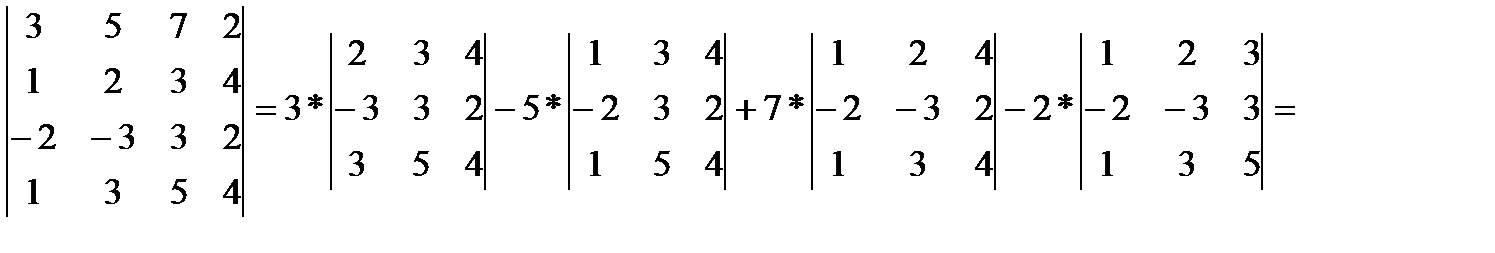
Вычисляем определители третьего порядка методом треугольника и получаем:

б) Вычислить, получив предварительно нули в первом столбце. Для этого, выберем ведущий элемент, находящийся во второй строке и первом столбце, элемент  .Обнуляем столбец. Прибавим к первой строке вторую, умноженную на (-3). Прибавим к третьей строке вторую, умноженную на 2.
.Обнуляем столбец. Прибавим к первой строке вторую, умноженную на (-3). Прибавим к третьей строке вторую, умноженную на 2.
Прибавим к четвертой вторую, умноженную на (-1). Получим:

Разложим определитель по элементам первого столбца. Получим:

По свойству определителей, общий множитель строки(столбца), можно вынести за знак определителя. Вынесем (-10) из четвертого столбца.

Методом треугольника вычисляем определитель третьего порядка. Получаем:
= 
2. Проверить совместность системы и в случае совместности решить её:
а)методом Крамера
б)матричным методом
в)методом Гаусса
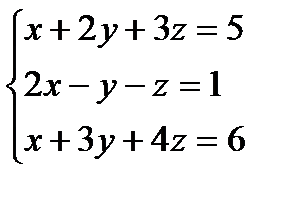
Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы этой системы равен рангу расширенной матрицы системы. Найдем ранг расширенной матрицы. Приведем расширенную матрицу к ступенчатому виду.
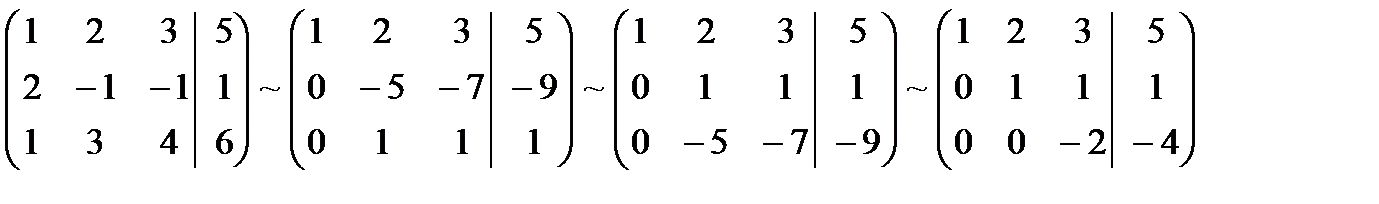 Ранг расширенной матрицы равен количеству элементов, стоящих на главной диагонали ступенчатой матрицы, равен 3.
Ранг расширенной матрицы равен количеству элементов, стоящих на главной диагонали ступенчатой матрицы, равен 3.
Так как ранг расширенной матрицы и ранг основной равны, то система совместна.
а) Решим систему метом Крамера.

Проверка.

б)Решим систему матричным методом.
Составим матрицу, состоящую из коэффициентов при неизвестных, назовем ее основной, обозначим А. Составим матрицу-столбец, состоящую из свободных членов, обозначим В. Составим матрицу –столбец, состоящую из переменных (неизвестных), обозначим Х.

Запишем систему линейных уравнений в матричном виде: 
Выразим Х: 
Для того, чтобы найти решение системы, необходимо найти обратную матрицу  .
.
Найдем обратную матрицу:
1) Вычислим определитель основной матрицы 
2) Найдем транспонированную матрицу, заменив в основной матрице строки столбцами: 
3) Найдем союзную матрицу, состоящую из алгебраических дополнений к каждому элементу транспонированной матрицы: 
4) Найдем обратную матрицу по формуле:  и подставим в Х, получим:
и подставим в Х, получим:  .
.
в) Решим систему методом Гаусса.
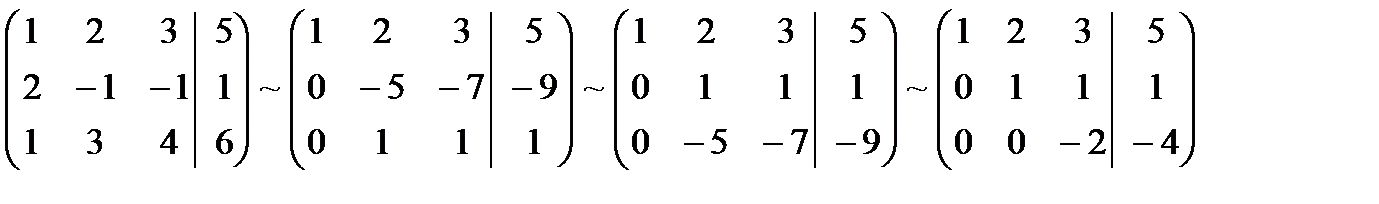 Вернемся к системе уравнений.
Вернемся к системе уравнений.
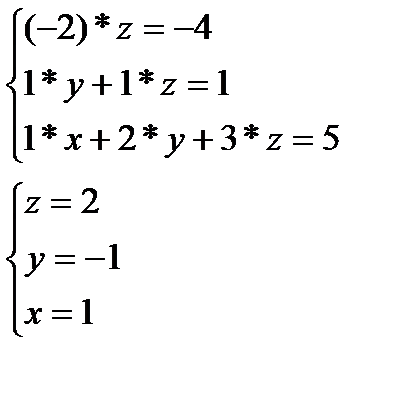
3. Решить матричное уравнение. 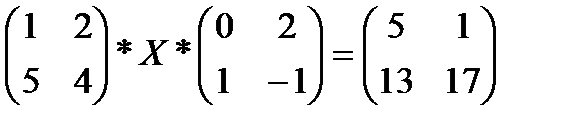
Для начала запишем наше матричное уравнение в буквенном виде: 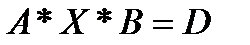
Выразим Х: 
Следовательно, для того, чтобы найти решение, необходимо найти обратные матрицы 
1)Найдем  .
.

2) Найдем  .
.

3) Найдем Х:

4. Выясните, образуют ли векторы  базис. Если образуют, то разложите вектор
базис. Если образуют, то разложите вектор  по этому базису.
по этому базису.
 .
.
Выясним, образуют ли векторы базис. Составим из координат векторов определитель 3-го порядка.

Так как определитель не равен 0, то векторы образуют базис. Найдем разложение вектора  по базису
по базису  .
.


Решим данную систему методом Крамера.

5.Заданы вершины треугольника АВС. Вычислите его площадь и косинус внутреннего угла А..

Треугольник АВС образован векторами 
Площадь треугольника 
Вычислим векторное произведение:

Вычислим косинус внутреннего угла при вершине А.

6.Найдите объем параллелепипеда, построенного на векторах  , если
, если 
Объём параллелепипеда, построенного на векторах  , равен
, равен  . Найдем векторы:
. Найдем векторы:


7.В треугольнике АВС составьте уравнения:
1) стороны ВС;
2) высоты, опущенной из вершины А на сторону ВС;
3) медианы, проведенной из вершины С.

1)Для того, чтобы составить уравнение стороны ВС необходимо воспользоваться следующей формулой: (уравнение прямой, проходящей через 2 точки)

2)Так как высота АН перпендикулярна стороне ВС, то  . Угловой коэффициент ВС:
. Угловой коэффициент ВС:  . Следовательно,
. Следовательно,  . Зная угловой коэффициент и точку, через которую проходит прямая можно составить уравнение высоты (прямой АН), используя следующую формулу:
. Зная угловой коэффициент и точку, через которую проходит прямая можно составить уравнение высоты (прямой АН), используя следующую формулу:

3)Медиана, проведенная из вершины С, делит сторону АВ пополам точкой М.
 . Можем составить уравнение медианы СМ.
. Можем составить уравнение медианы СМ.

8.Напишите каноническое уравнение прямой, проходящей через точку А и перпендикулярной плоскости α.
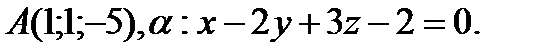
Каноническое уравнение прямой имеет вид:
 , где
, где  точка, через которую проходит прямая.
точка, через которую проходит прямая.  направляющий вектор прямой. Так как прямая проходит через точку А, перпендикулярно плоскости, то, вектор нормали
направляющий вектор прямой. Так как прямая проходит через точку А, перпендикулярно плоскости, то, вектор нормали  будет параллелен направляющему вектору
будет параллелен направляющему вектору  . Векторы параллельны, следовательно, координаты их пропорциональны. Тогда,
. Векторы параллельны, следовательно, координаты их пропорциональны. Тогда, 
| l |

|

|
| А |
Уравнение прямой будет иметь вид:

9. Нарисуйте область, ограниченную заданными поверхностями.

|
| X=0 |
| Y=0 |
| Z=0 |
| Z |
| Y |
| X |

Матрица
Матрица – это прямоугольная таблица элементов, содержащая m строк и n столбцов.
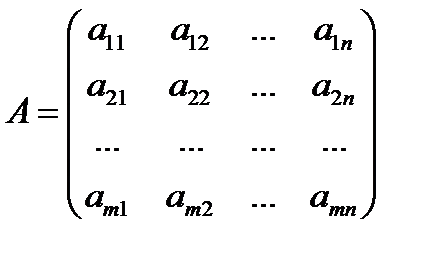
Матрица А называется матрицей размера mxn, числа aiJ называются ее элементами, где i показывает номер строки, а j – номер столбца. Числа а11, а22, а33… образуют главную диагональ.
Классификация матриц
- Две матрицы равны между собой, если равны все соответствующие элементы этих матриц.
- Матрица называется квадратной, если число строк равно числу столбцов. При этом квадратную матрицу размера nxn называют матрицей n-го порядка.
- Квадратная матрица называется диагональной, если все элементы, кроме элементов главной диагонали, равны нулю.

- Диагональная матрица называется единичной, если все элементы главной диагонали равны единице.

- Матрица называется нулевой, если все элементы равны нулю.

- Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.

- Матрица называется транспонированной к данной, если каждая строка данной матрицы становится столбцом с тем же номером у новой матрицы. Обозначается Ат.
 :
:
 2017-11-01
2017-11-01 557
557







