2017-11-01
666
1. Метод Гаусса (расширенную матрицу с помощью элементарных преобразований свести к ступенчатой, а потом к канонической)
К элементарным преобразованиям относятся:
- перестановка строк (столбцов)
- прибавление к одной строке (столбцу) другой, умноженной на число, отличное от 0.
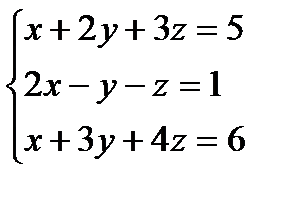
Составим расширенную матрицу:
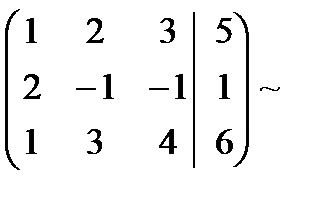
Выберем ведущий элемент, стоящий в первом столбце и первой строке, элемент 1., назовем его ведущим. Строка, в которой находится ведущий элемент меняться не будет. Обнулим элементы под главной диагональю. Для этого прибавим ко второй строке первую, умноженную на (-2). Прибавим к третьей строке первую, умноженную на (-1), получим:
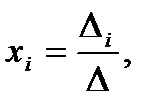
Поменяем вторую и третью строки местами. Мысленно вычеркиваем первый столбец и первую строку и продолжаем алгоритм для оставшейся матрицы. К третьей строке прибавляем 2-ю, умноженную на 5.
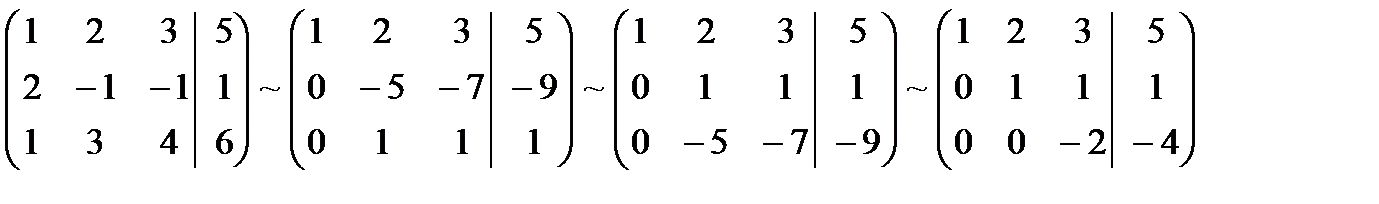
Привели расширенную матрицу к ступенчатому виду. Возвращаясь к уравнениям системы, начиная с последней строки и двигаясь вверх, поочередно определяем неизвестные.
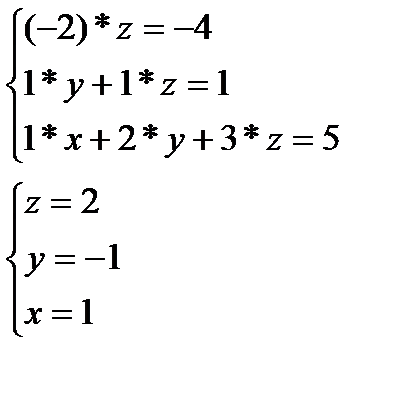
2. Матричный метод (AX=B, A-1AX=A-1B, X=A-1B; матрицу, обратную к основной матрице умножить на столбец свободных членов)
3. Метод Крамера.
Решение системы находится по формуле:
Где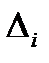 
-определитель измененной основной матрицы, в которой i-й столбец изменен на столбец свободных членов, а 
- главный определитель, состоящий из коэффициентов при неизвестных.
Векторы.
Вектор – это направленный отрезок
Любой вектор задается длиной (модулем) и направлением.
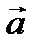
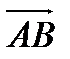
Обозначение: или
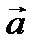
где А – начало вектора, В – конец вектора, – длина вектора.
