Этот метод заключается в том, что заменяют переменную х на 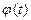 ,где
,где 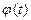 -непрерывно дифференцируемая функция, полагают
-непрерывно дифференцируемая функция, полагают 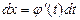 и получают
и получают 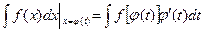
При этом получают искомую функцию, выраженную через переменную t. Для возвращения к переменной х необходимо заменить t значением 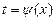 , которое находится из соотношения
, которое находится из соотношения 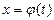 .
.
Рассмотрим нахождение интегралов методом подстановки.
Пример 1: Найти неопределенный интеграл 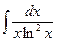
Решение: 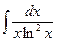 =
= 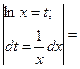
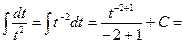
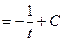
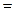
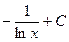

Пример 2: Найти неопределенный интеграл 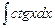
Решение: 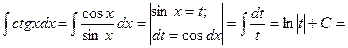
= 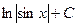
Пример 3: Найти неопределенный интеграл 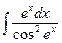
Решение: 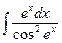 =
= 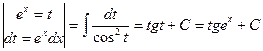
Пример 4: Найти неопределенный интеграл 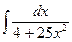
Решение: 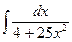 =
= 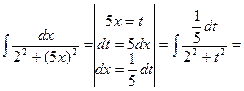
= 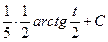 =
= 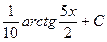 .
.
Определенный интеграл и его свойства
Пусть функция 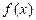 определена на отрезке
определена на отрезке 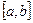 . Разобьем отрезок на n частей точками
. Разобьем отрезок на n частей точками 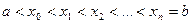 , выберем на каждом элементарном отрезке
, выберем на каждом элементарном отрезке 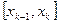 произвольную точку xk и обозначим через
произвольную точку xk и обозначим через 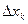 длину каждого такого отрезка.
длину каждого такого отрезка.
Интегральной суммой для функции 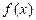 на отрезке
на отрезке 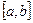 называется сумма вида
называется сумма вида
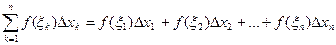
Определение 3.3: Определенным интегралом от функции 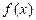 на отрезке
на отрезке 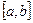 называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
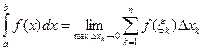
Для любой функции 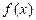 , непрерывной на отрезке
, непрерывной на отрезке 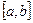 , всегда существует определенный интеграл
, всегда существует определенный интеграл 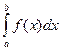
 2017-11-01
2017-11-01 3231
3231
