2017-11-01
739Методические указания и задания
По выполнению расчетно-графической работы
для подготовки студентов очной и заочной форм обучения
по дисциплине «Математика»
Раздел «Дифференциальное исчисление»
Кумертау 2016
Содержание
Введение. 4
1. Указания к выполнению расчетно-графической работы. 5
2. Решение типового варианта. 6
3. Варианты индивидуальных заданий. 19
Список литературы: 42
Введение
Дифференциальное исчисление функции одной переменной является фундаментом, на котором строятся методы исследования задач, предъявляемых практикой.
Методические указания к выполнению типовой расчетной работы по теме «Дифференцирование функции одной переменной и его приложения» содержат большое количество решенных задач, в которых рассматриваются методы дифференциальных функций, заданных различными способами. Рассмотрены различные приложения дифференциального исчисления функции одной переменной к геометрии.
Методические указания к выполнению типовой расчетной работы по теме «Дифференцирование функции одной переменной и его приложения» для студентов всех специальностей и направлений (очное и заочное обучение).
|
|
|
Указания к выполнению расчетно-графической работы.
При подготовке к выполнению расчетно-графической работы студенту рекомендуется изучить теоретический материал, согласно программе и по указанной литературе.
Варианты контрольных работ распределяются по последней цифре зачетной книжки студента.
При выполнении контрольной работы и ее оформлении следует придерживаться следующих правил:
1. На титульном листе указать Ф. И. О. студента, его специальность и номер варианта.
2. Перед решением задачи необходимо записать полный текст ее условия.
3. Решение записывать аккуратно, соблюдая поля для замечаний рецензента.
4. Решение сопровождается четкими пояснениями.
5. Решение должно быть подробным.
Если в работе есть существенные ошибки, то она получает оценку "не зачет". В этом случае студенту следует выполнить работу над ошибками в той же тетради, в которой была решена расчетно-графическая работа.
2. Решение типового варианта
Задача 1. Приведите пример бесконечного множества, из которого можно выделить счетное подмножество.
Решение:
Пример первый. Рассмотрим множество Z-множество целых чисел, оно бесконечное 
а множество натуральных чисел N является счетным и вместе с тем является подмножеством множества Z, т.е.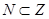 
Пример второй. Рассмотрим множество рациональных чисел(это числа вида 
, где 
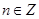и 
и 
) очевидно Q – бесконечное множество, а множество Z счетное и является подмножеством множества Q, т.к. 
.
|
|
|
Задача 2.
а) Используя определение предела числовой последовательности по Коши, доказать, что
;
б) Используя определение предела функции по Коши, доказать, что 
. Найти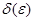 
, если 
.
Решение:
а) чтобы доказать, что (1) по определению предела числовой последовательности по Коши, надо доказать, что для 
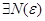такое, что при 
будет справедливо неравенство 
(2). Чтобы найти N(
), решим неравенство (2):
(3)
Заметим, что 
при 
и 
при 
имеем 
. За номер 
примем наибольшее целое число не превосходящее 
, оно обозначается 
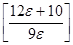и называется антье числа .
Итак, показали, что для 
такой, что при 
справедливо неравенство (2) 
по определению предела числовой последовательности.
б) Чтобы доказать что , надо доказать, что для 
такое, что при 
. будет справедливо неравенство 
(3).
находят из неравенства (3):
. Меньшее из 2х чисел 
и 
примем за 
, т.е. 
, где 
.
Итак, доказали, что для 
такое, что для 
, удовлетворяющих неравенству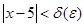 
будет выполняться неравенство (3) 
по определению предела функции. Если 
, то 
.
Задача 3. Найти пределы:
а) 
| б) 
|
в) 
| г) 
|
д)  .
|
Решение:
Сначала заметим, что в задаче 3 используем следующую теорему алгебры: "Если многочлен целой степени относительно 
имеет все коэффициенты целые, а старший коэффициент равен единице и если этот многочлен имеет целые корни, то они являются делителями свободного члена". Из этой теоремы следует, что целые корни вышеуказанного многочлена надо искать среди делителей свободного члена. Кроме того, известно, что если число 
является корнем многочлена, то он без остатка делится на 
.
Для того чтобы выполнить задание:
а) следует разложить на множители 
и 
, т.к. в этом задании имеем неопределенность вида 
. Многочлен имеет корень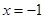 
без остатка делится на 
, выполним это деление
Следовательно 
Найдем корни многочлена , для этого решаем уравнение 
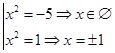
Итак 
.
б) 
.
в) 
.
г) 
д) 
, т.к. 
, это следствие из 2го замечательного предела.
Задача 4. Пользуясь методом замены бесконечно малых величин эквивалентными, найти 
.
Решение:
Известно, что при 
и 
.
Задача 5. Найти точки разрыва функции 
и выяснить какого они рода.
Решение:
Точка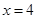 
есть точка разрыва данной функции, т.к. в этой точке функции не существует.
Следовательно 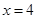- точка разрыва 1го рода, причем скачок функции равен 
.
Задача 6. Найти производные функций:
а)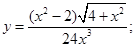 
| б) 
|
в)  .
|
Решение:
Все производные берем по правилам и формулам дифференцирования.
а)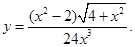 
б) 
в)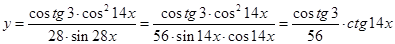 
Задача 7. Найти вторую производную 
от функции, заданной параметрически:
.
Решение:
Известно, что если функция задана параметрически, т.е. в виде 
, то ее первая производная берется по формуле 
, а вторая производная по формуле:
.
Задача 8. Вычислить приближенно с помощью дифференциала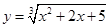 
, 
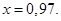
Решение:
Примем за 
, за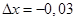 
, тогда 
.
Известно, что 
Итак, 
при 
.
Задача 9. Найти дифференциал второго порядка от функции 
.
Решение:
, где 
.
.
Задача 10. Провести полное исследование функции и на основании исследования схематически построить график функции:
а) 
| б) 
|
а) Исследуем функцию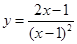 
1) 
точка разрыва, выясним какого она рода, для этого найдем 
и 
. В данном случае они равны 
точка разрыва 2го рода 
вертикальная асимптота.
2) Найдем точки пересечения графика функции с осями координат. При 
- точка пересечения графика функции с осью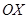 
. При 
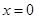
- точка пересечения графика функции с осью 
.
3) Данная функция не обладает свойством четности (т.к. 
) и свойством нечетности (т.к. 
).
4) Исследуем функцию на монотонность и экстремум. Найдем производную данной функции 
.
Заметим, что существует при 
и 
при 
- точка подозрительная на экстремум.
|
|
|
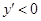
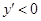
0 1
В 
в этих промежутках функция убывает по достаточному признаку убывания функции в промежутке.
В 
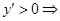в этом промежутке функция возрастает по достаточному признаку возрастания функции в промежутке. 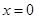точка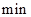 
по достаточному признаку существования экстремума функции в точке и 
.
Полученные результаты полезно поместить в таблице.
|
| 
|
| 
| ||
| - | + | не сущ | - | |
| 
|
| 
| не сущ | 
|
5) Исследуем функцию на выпуклость (вогнутость) и точки перегиба.
Итак, 
Возьмем вторую производную от данной функции:
Заметим, что 
существует при и 
при 
точка 
точка подозрительная на перегиб.
0 1
В 
в этом промежутке функция выпукла по достаточному признаку выпуклости функции в промежутке.
В 
в этих промежутках функция вогнута по достаточному признаку вогнутости функции в промежутке. - абсцисса точки перегиба 
- точка перегиба.
Полученные результаты поместим в таблице:
|
| 
|
| 
| 
|
|
|
| - | + | не сущ | + | |
|
| 
|
| 
| не сущ | 
|
6) Найдем невертикальные асимптоты в виде 
, где 
. В нашем случае 
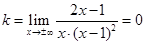и 
- горизонтальная асимптота при 
.
7) На основании исследования построим график функции (сначала следует построить асимптоты, затем характерные точки, точки пересечения с осями координат, точки экстремума, точки перегиба).
б) Исследуем функцию 
1) 
точка разрыва, выясним какого она рода, для этого найдем 
и 
.
точка разрыва 2го рода и 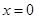вертикальная асимптота.
2) Найдем точки пересечения графика функции с осями координат.
Поскольку 
, то график функции не пересекается с осью . При 
- точка пересечения графика функции с осью .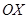
3) Функция не обладает свойством четности (т.к. ) и свойством нечетности (т.к. ).
4) Исследуем функцию на монотонность и экстремум.
Заметим существует при , кроме 
, но в точке она не существует, т.к. 
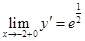, а 
, заметим также, что нет точек в области определения функции, в которых 
точка подозрительная на экстремум.
|
|
|
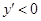
-2 0
В 
в этом промежутке функция убывает. В 
в этих промежутках функция возрастает. - точка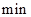 
.
Полученные результаты поместим в таблице:
|
|
| -2 | 
| 
| |
|
| - | не сущ | + | + | |
|
|
|
| 
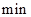| не сущ | 
|
4) Исследуем функцию на выпуклость (вогнутость) и точки перегиба.
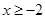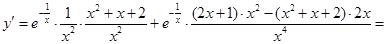
Найдем сначала при 
.
при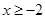
Итак, 
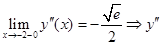не существует при
при 
точки и 
являются точками подозрительными на перегиб.
-2 0 
В 
в этих промежутках функция выпуклая.
В 
в этих промежутках функция вогнута.
и абсциссы точек перегиба 
.
Итак,
|
| 
| 
|
| 
| 
|
| 
| ||||||||||||
|
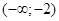| - | не сущ | + | + | - | ||||||||||||||
|
|
|
|
| не сущ |
|
|
|
5) Найдем невертикальные асимптоты в виде .
аналогично
Итак, 
асимптота при 
асимптота кривой при 
.
6) На основании исследования строим график функции.
Варианты индивидуальных заданий
Вариант 1
Задача 1. Доказать, что множество 
ограничено. Установить какие числа являются гранями. Найти точную верхнюю и точную нижнюю грани этого множества, а также наибольший и наименьший элементы множества.
Задача 2.
а) Используя определение предела числовой последовательности по Коши, доказать, что 
;
б) используя определение предела функции по Коши, доказать, что 
. Найти 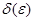, если 
.
Задача 3. Вычислить предел функции:
а) 
;
б) 
;
в) 
;
г) 
;
д) 
.
Задача 4. Пользуясь методом замены бесконечно малых величин эквивалентными, найти 
.
Задача 5. Найти точки разрыва функции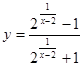 
, выяснить какого они рода.
Задача 6. Найти производные функции
а) 
;
б) 
;
в) 
.
Задача 7. Найти вторую производную от функции, заданной параметрически 
.
Задача 8. Вычислить приближенно с помощью дифференциала 
.
Задача 9. Найти дифференциал второго порядка от функции 
.
Задача 10. Провести полное исследование функции и на основании исследования схематически построить график функции
а) 
;
б) 
.
Вариант 2
Задача 1. Доказать, что множество 
ограничено. Установить какие числа являются его гранями. Найти точные верхнюю и нижнюю грани этого множества, а также наибольший и наименьший элементы множества
Задача 2.
а) Используя определение предела числовой последовательности по Коши, доказать, что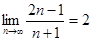 
;
б) Используя определение предела функции по Коши, доказать, что 
. Найти 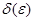, если 
.
Задача 3. Найти пределы:
а) 
;
б) 
;
в) 
;
г) 
;
д) 
.
Задача 4. Пользуясь методом замены бесконечно малых величин эквивалентными, найти 
.
Задача 5. Найти точки разрыва функции 
и выяснить какого они рода.
Задача 6. Найти производные функций
а) 
;
б) 
;
в) 
.
Задача 7. Найти вторую производную 
от функции, заданной параметрически 
.
Задача 8. Вычислить приближенно с помощью дифференциала 
.
Задача 9. Найти дифференциал второго порядка от функции 
.
Задача 10. Провести полное исследование функции и на основе исследования схематически построить график функции
а)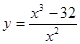 
;
б) 
.
Вариант 3
Задача 1. Приведите пример числового множества X, у которого:
а) 
;
б) 
.
Задача 2.
а) По определению предела числовой последовательности по Коши, доказать, что 
;
б) По определению предела функции по Коши, доказать, что 
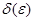. Найти , если .
Задача 3. Найти пределы:
а) 
;
б) 
;
в)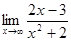 
;
г) 
;
д) 
.
Задача 4. Пользуясь методом замены бесконечно малых величин эквивалентными, найти 
;
Задача 5. Найти точки разрыва функции 
и выяснить какого они рода.
Задача 6. Найти производные функций:
а) 
;
б) 
;
в) 
.
Задача 7. Найти вторую производную от функции, заданной параметрически 
.
Задача 8. Вычислить приближенно с помощью дифференциала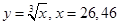 
.
Задача 9. Найти дифференциал второго порядка от функции 
.
Задание 10. Провести полное исследование функции и на основании исследования схематически построить график функции:
а) 
;
б) 
.
в)
Вариант 4
Задача 1. Приведите пример числового множества X, у которого:
а) 
;
б) .
Задача 2.
а) Используя определение предела числовой последовательности по Коши, доказать, что 
;
б) Используя определение предела функции по Коши, доказать, что 
. Найти 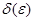, если =0,01.
Задача 3. Найти пределы:
а) 
;
б) 
;
в) 
;
г) 
;
д) 
.
Задача 4. Пользуясь методом замены бесконечно малых величин эквивалентными, найти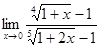 
.
Задача 5. Найти точки разрыва функции 
и выяснить какого они рода.
Задача 6. Найти производные функции:
а) 
;
б) 
;
в)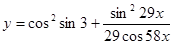 
.
Задача 7. Найти вторую производную функции заданной параметрически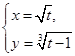 
.
Задача 8. Вычислить приближенно с помощью дифференциала 
.
Задача 9. Найти дифференциал второго порядка от функции, заданной неявно 
.
Задача 10. Провести полное исследование функции и на основании исследования схематически построить график функции:
а) 
;
б)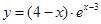 
.
Вариант 5
Задача 1. Приведите пример счетного множества, из которого можно выделить счетное подмножество.
Задача 2.
а) Используя определение предела числовой последовательности по Коши, доказать, что 
;
б) Используя определения предела функции по Коши, доказать, что 
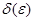. Найти , если .
Задача 3. Найти пределы:
а) 
;
б) 
;
в) 
;
г) 
;
д)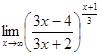 
.
Задача 4. Пользуясь методом замены бесконечно малых величин эквивалентными, найти 
.
Задача 5. Найти точки разрыва функции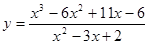 
и выяснить какого они рода.
Задача 6. Найти производные функций:
а) 
;
б) 
;
в) 
.
Задача 7. Найти вторую производную от функции заданной параметрически 
.
Задача 8. Вычислить приближенно с помощью дифференциала 
.
Задача 9. Найти дифференциал второго порядка от функции 
.
Задача 10. Провести полное исследование функции и на основании исследования схематически построить график функции
а) 
;
б)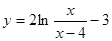 
.
Вариант 6
Задача 1. Приведите примеры счетных множеств. Эквивалентны ли множества 
и 
, является ли одно из них подмножеством другого?
Задача 2.
а) Используя определение предела числовой последовательности по Коши, доказать, что 
;
б) Используя определение предела функции по Коши, доказать, что 
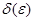. Найти , если 
.
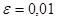Задача 3. Найти пределы:
а)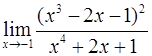 
;
б) 
;
в) 
;
г) 
;
д) 
.
Задача 4. Пользуясь методом замены бесконечно малых величин эквивалентными, найти 
.
Задача 5. Найти точки разрыва функции 
и выяснить какого они рода.
Задача 6. Найти производные функций:
а)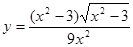 
;
б) 
;
в) 
.
Задача 7. Найти вторую производную от функции, заданной параметрически 
.
Задача 8. Вычислить Приближенно с помощью дифференциала 
.
Задача 9. Найти дифференциал второго порядка от функции 
.
Задача 10. Провести полное исследование функции, и на основании исследования схематически построить график функции:
а) 
;
б) 
.
Вариант 7
Задача 1. Приведите пример числового множества X, у которого:
а) ;
б) 
.
Имеет ли это множество X в случае а) и б) наименьший элемент?
Задача 2.
а) Используя определение предела числовой последовательности по Коши, доказать, что 
;
б) Используя определение предела функции по Коши, доказать, что 
. Найти 
, если 
.
Задача3. Найти пределы:
а) 
;
б) 
;
в) 
;
г) 
;
д) 
.
Задача 4. Пользуясь методом замены бесконечно малых величин эквивалентными, найти 
.
Задача 5. Найти точки разрыва функции 
и выяснить какого они рода.
Задача 6. Найти производные функций:
а) 
;
б) 
;
в) 
.
Задача 7. Найти вторую производную от функции, заданной параметрически 
.
Задача 8. Вычислить приближенно с помощью дифференциала 
.
Задача 9. Найти дифференциал второго порядка от функции 
Задача 10. Провести полное исследование функции и на основании исследования схематически построить график функции:
а) 
;
б) 
.
Вариант 8
Задача 1. Докажите, что множество [0;1]~[a;b], где a и b произвольные числа 
.
Задача 2.
а) Используя определение предела числовой последовательности по Коши, доказать, что 
;
б) Используя определение предела функции по Коши, доказать, что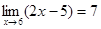 
. Найти
