2017-10-25
568
3. 1. – 3.10. Найти пределы функций, не пользуясь правилом Лопиталя.
3.1. а)  ;
| б)  ;
|
в)  ;
| г)  .
|
3.2. а)  ;
| б)  ;
|
в)  ;
| г)  .
|
3.3. а)  ;
| б)  ;
|
в)  ;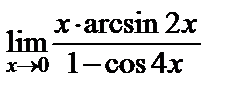
| г)  .
|
3.4. а)  ;
| б)  ;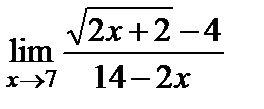
|
в)  ;
| г)  .
|
3.5.а)  ;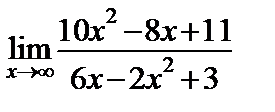
| б)  ;
|
в)  ;
| г)  .
|
3.6.а)  ;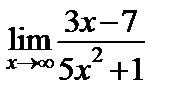
| б)  ;
|
в)  ;
| г)  .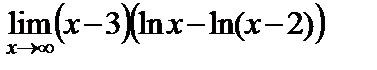
|
3.7.а)  ;
| б)  ;
|
в)  ;
| г)  .
|
3.8.а)  ;
| б)  ;
|
в)  ;
| г)  .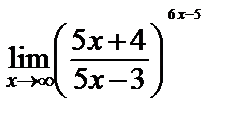
|
3.9. а)  ;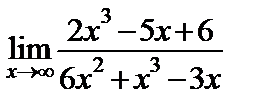
| б)  ;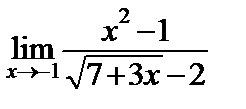
|
в)  ;
|
г)  .
|
3.10. а)  ;
| б)  ;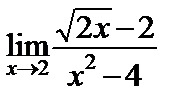
|
в)  ;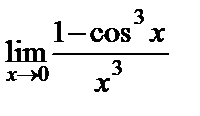
| г)  .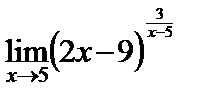
|
3.11. – 3.20. Задана функция 
. Требуется: 1) исследовать на непрерывность; 2) классифицировать точки разрыва функции, если они существуют; 3) исследовать поведение функции на бесконечности; 4) сделать схематический чертеж по результатам исследования.
3.11. а)  ;
| б)  .
|
3.12.
а)  ;
| б)  .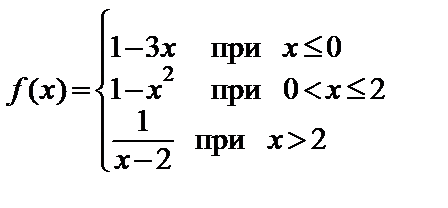
|
3.13. а)  ;
| б)  .
|
3.14. а)  ;
| б)  .
|
3.15. а)  ;
| б)  .
|
3.16. а)  ;
| б)  .
|
3.17. а)  ;
| б)  .
|
3.18. а)  ;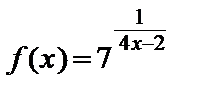
| б)  .
|
3.19. а)  ;
| б)  .
|
3.20. а)  ;
| б) 
|
