Пример заданий контрольной работы №1

УТВЕРЖДАЮ

Ректор университета

____________ О.Н. Федонин

«» ____________ 2017 г.

 

 

МАТЕМАТИКА

 

Методические указания к выполнению

заданий расчетно-графической работы для

студентов I курса очной формы обучения

по направлениям подготовки 11.00.00 «Электроника,

радиотехника и системы связи», 13.00.00 «Электро- теплоэнергетика», 15.00.00 «Машиностроение»,

27.00.00 «Управление в технических системах»

 

 

(I семестр)

 

Брянск 2017

 

УДК 511

 

Математика [Текст]+[Электронный вариант]: Методические указания к выполнению заданий расчетно-графической работы для студентов I курса очной формы обучения по направлениям подготовки 11.00.00 «Электроника, радиотехника и системы связи», 13.00.00 «Электро- теплоэнергетика», 15.00.00 «Машиностроение», 27.00.00 «Управление в технических системах» (I семестр). − Брянск: БГТУ, 2017. − 30с.

 

Разработали: Н.А. Ольшевская, доц.

Г.Г. Цуленева, доц.

 

 

Рекомендовано кафедрой “Высшая математика” БГТУ

(протокол № 1 от 5.09.17)

 

 

Методические указания публикуются в авторской редакции

 

СОДЕРЖАНИЕ

Введение…………………………………………………………….4

Задания к расчетно-графической работе……………………...….5

Пример заданий контрольной работы №1……………………....21

Пример заданий контрольной работы №2……………………....22

Теоретические вопросы к экзамену……………………………...22

Пример практической части экзаменационного билета………..24

Открытый банк экзаменационных заданий……………………..25

Список рекомендуемой литературы……………………………..31

 

 

ВВЕДЕНИЕ

 

Настоящие методические указания ориентированы на студентов первого курса очной формы обучения инженерно-технических направлений подготовки. Они содержат задания к расчетно-графической работе, примеры заданий контрольных работ, теоретические вопросы для подготовки к экзамену и вариант его практической части, а также открытый банк экзаменационных задач.

В работе приведены примеры решения наиболее сложных задач, это задачи №7 и №8 РГР.

Перед решением задач №3,4,5 рекомендуем разобрать аналогичные решенные задачи, приведенные в методических указаниях [6].

 

 

ЗАДАНИЯ К РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЕ

Задание №1

 

Решить систему линейных алгебраических уравнений тремя методами:

а) по правилу Крамера; б) методом Гаусса; в) с помощью обратной матрицы.

 

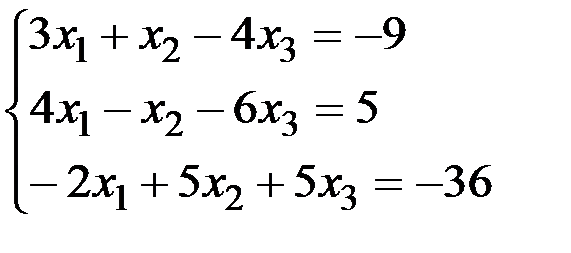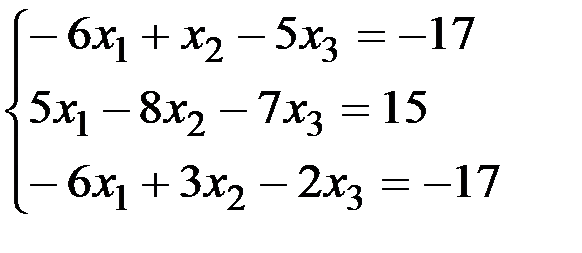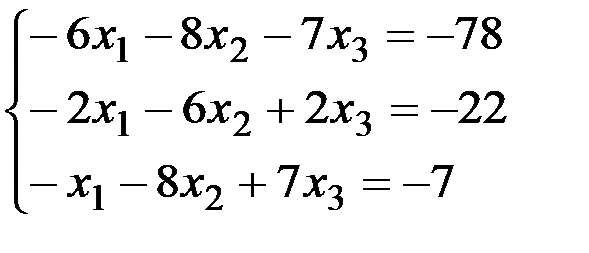Задание №2

Решить следующую задачу.

1. Определить модуль равнодействующей двух равных по модулю сходящихся сил |F₁|=|F₂|=5Н, образующих между собой угол .

y

x

F2

Рис.1

F1

2. Определить угол в градусах между равнодействующей двух сил и осью Ох, если угол 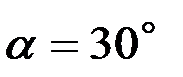(рис.1).

R

F1

y

x

F2

Рис.2

3. Равнодействующая R двух равных по модулю сходящих сил направлена по оси Оу и равна по модулю 10Н. Определить в градусах угол, образованный вектором силы с положительным направлением оси Ох (рис.2).

 

y

x

F2

Рис.3

F1

F3

4. Определить модуль равнодействующей сходящихся сил

, если известны углы, образованные векторами этих сил с осью Ох:

t ABQABgAIAAAAIQA4/SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQIt ABQABgAIAAAAIQBYyGzEdgcAAOg7AAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBL AQItABQABgAIAAAAIQDe8IaN3wAAAAkBAAAPAAAAAAAAAAAAAAAAANAJAABkcnMvZG93bnJldi54 bWxQSwUGAAAAAAQABADzAAAA3AoAAAAA ">

y

x

F2

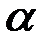Рис.4

F1

F3

(рис.3).

 

5. Какую по модулю силу F₃ надо приложить к сходящимся силам образующим с осью Ох углы , чтобы равнодействующая этих трех сил равнялась нулю (рис.4)?

 

y

x

F2

Рис.5

F1

R

6. Равнодействующая |R|=10Н двух сходящихся сил образует с осью Ох угол . Сила |F₁|=5Н образует с этой же осью Ох угол . Определить модуль силы |F₂| (рис.5).

 

А

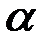x

y

F2

F1

Рис.6

7. На твердое тело в точке А действуют силы F₁ и F₂, |F₁|=6H, |F₂|=3H, линии действия которых в плоскости Оху. Определить сумму проекций этих сил на ось Ох, если угол (рис. 6).

 

F1

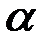F2

Рис.7

8. На пресс в точке О действуют силы F₁ и F₂, линии действия которых находятся в плоскости чертежа (рис.7). Определить модуль вертикальной силы, сжимающей материал, если заданы углы .

 

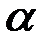F1

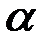F2

x

F3

x

Рис.8

y

A

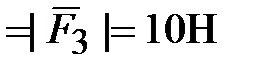9. К столбу в точке А приложена плоская система сходящихся сил . Определить

сумму проекций заданных сил на ось Ах, если (рис. 8).

 

 

Рис.9

х

y

F3

F2

F1

10. На твердое тело в точке О действует плоская система сходящихся сил

. Определить сумму проекций заданных сил на ось Оу, если заданы углы (рис. 9).

11. Для плоской системы сходящихся сил F₁=3 i +4 j; F₂=5 j; F₃=2 i определить модуль равнодействующей силы и угол, который она образует с положительным направлением оси Ох.

12. Равнодействующая сходящихся сил F₁ и F₂ равна по модулю 8Н и образует с горизонтальной осью угол . Вектор силы F₁направлен по оси Ох, а вектор силы F₂ образует с этой осью угол . Определить модуль силы F₁.

13. Плоская система трех сходящихся сил F₁, F₂ и F₃ находится в равновесии. углы, образованные векторами сил F₁ и F₂ с положительным направлением горизонтальной оси Ох, соответственно равны . Определить модуль силы F₃.

14. Задана проекция R_x=5Н равнодействующих двух сходящихся сил F₁ и F₂ на горизонтальную ось Ох. Проекция силы F₁ на эту же ось F_1x=7Н. Определить алгебраическое значение проекции на ось Ох силы F₂

15. Определить модуль равнодействующей сходимости сил F₁ и F₂, если известны их проекции на декартовы оси координат: F_1x=3H, F_1y=6H, F_2x=5H, F_2y=4H.

16. Определить, сходится ли данная плоская система трех сходящихся сил в равновесии, если известны проекции сил на оси координат: F_1x=10H, F_1y=2H, F_2x= -4H, F_2y=3H, F_3x= -6H, F_3y= -5H.

17. Равнодействующая плоской системы сходящихся сил F₁ и F₂,F₃ и F₄ равна 0. Определить модуль силы F₁, если известны проекции трех других сил на оси координат: F_2x= 4H, F_2y=7H, F_3x= -5H, F_3y= -5H, F_4x= -2H, F_4y=0.

F1

Рис.10

F2

a

y

x

18. Известны проекции на оси R_x=18Н, R_у=24Н равнодействующей R плоской системы сходящихся сил F₁, F₂ и F₃, а также проекции сил на F₂ и F₃ на эти же оси: F_2x= -9H, F_2y= -7H, F_3x= 12H, F_3y=0. Определить модуль силы F₁.

19. Определить в градусах угол между вектором равнодействующей R системы сил F₁=3 i +2 j; F₂=5 i +7 j и положительным направлением оси Оу.

20. Определить модуль равнодействующей двух сил угол , угол (рис.10).

21. Определить угол, который образует равнодействующаяR с положительным направлением оси Оу, если угол , угол (рис.11).

F3

x

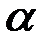Рис.12

F1

F2

y

22. На твердое тело в точке О действует плоская система сходящихся сил. Определить сумму проекций заданных сил на ось Ох, если заданы

,угол (рис.12).

23. Равнодействующая R=10Н двух сходящихся сил образует с вертикальной осью угол . . Найти (рис.13).

Рис.13

F1

F2

y

x

24. Равнодействующая двух сходящихся сил F₁ и F₂ образует с осью Ох угол

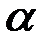R=8Н, . Построить силу , определить ее модуль и направляющие углы (рис. 14).

Рис.14

F1

R

y

x

25. Даны три сходящихся силы F₁, F₂, F₃. . Эти силы образуют с осью Ох углы: . Найти силу S, уравновешивающую систему сил F₁, F₂, F₃.

26. По заданным проекциям силы F на оси координат F_х=20Н, F_у=25Н, F_z=30Н определить модуль этой силы.

Рис.15

x

R

z

y

27. Определить косинус угла между вектором силы F и осью координат Оz, если сила F=3 i +4 j +5 k.

28. Определить косинус угла между вектором силы F=3 i +2,45 j +7 k и осью координат Ох.

29. Модуль равнодействующей R пространственной системы сходящихся сил равен 150Н. Определить ее проекцию на координатную ось Оу, если даны углы (рис.15).

30. Определить модуль равнодействующей сил , приложенных к точке А, как показано на рис 16.

F3

y

Рис.16

F1

А

F2

x

z

31. Определить модуль равнодействующей трех сходящихся сил, если заданы их проекции на оси координат: F_1x=7H, F_1y=10H, F_1z=0; F_2x= -5H, F_2y=15H, F_2z=12Н; F_3x=6H, F_3y=0, F_3z= -6Н.

32. Две силы F₁=5i+7j+9k иF₂=4i+9j+11k приложены в центре О системы прямоугольных координат О хуz. Определить модуль равнодействующей силы.

Задание №3

Даны координаты вершин пирамиды А₁ А₂ А₃ А_4.

Построить пирамиду.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂ и А₁ А₄;

3) площадь грани А₁А₂А₃;

4) объем пирамиды.

 

Вариант	А1	А2	А3	А4
	(2; 3; 2)	(10; 7; 3)	(6; 6; 3)	(8; 9; 5)
	(3; 5; 2)	(1; 7; 5)	(5; 6; 8)	(1; 6; 4)
	(6; 1; 4)	(3;-3; 8)	(5;-5; 8)	(8; 3; 3)
	(2; 5; 4)	(5; 3; 6)	(8; 3; 5)	(8; 2; 10)
	(3; 4; 3)	(7;-4; 4)	(6; 0; 4)	(9; 10; 6)
	(1; 2; 3)	(3; 4; 6)	(-3; 1; 6)	(3; 3; 5)
	(3; 5; 1)	(0; 1; 5)	(1; 0; 5)	(7; 9; -1)
	(5;-2; 4)	(7; 1; 6)	(7; 4; 5)	(8; 4; 10)
	(1; 2; 1)	(9;-2; 2)	(-3; 5; 0)	(7; 8;-2)
	(4; 1; 3)	(2; 3; 6)	(5;-3; 6)	(3; 3; 5)
	(3;-1; 2)	(7; 2; 6)	(9; 0; 6)	(5; 1; 3)
Вариант	А1	А2	А3	А4
	(3; 5; 4)	(1; 8; 6)	(-1; 2; 6)	(9;-1; 1)
	(1; 1; 2)	(-3;9; 3)	(-2; 5; 3)	(7; 7; -1)
	(1; 4; 3)	(-1; 6; 6)	(6; -4; 0)	(2; 2; 1)
	(2; 4; 1)	(6; 7; 5)	(7; 6; 5)	(6; 8; 3)
	(1; 2; 2)	(3; 5; 4)	(5;-1; 4)	(7; 8; 5)
	(2;-2; 1)	(10; 2; 2)	(6; 1; 2)	(8; 4; 4)
	(3; 4;-1)	(1; 6; 2)	(5; 5; 5)	(1; 5; 1)
	(2; 5; 3)	(-1; 1; 7)	(1; -1; 7)	(4; 7; 2)
	(1; 4; 2)	(4; 2; 4)	(7; 2; 3)	(7; 1; 8)
	(3; 1; 4)	(7; -7; 5;)	(6; -3; 5)	(9; 7; 7)
	(2; 4; 3)	(4; 6; 6)	(-2; 3; 6)	(4; 5; 5)
	(5;-2;-1)	(2; -6; 3)	(3; -7; 3)	(9; 2; -3)
	(5; 2; 1)	(7; 5; 3)	(7; 8; 2)	(8; 8; 7)
	(2;-1; 7)	(10;-5; 8)	(-2; 2; 6)	(8; 5; 4)
	(4; 7; 8)	(2; 9; 11)	(5; 3; 11)	(3; 9; 10)
	(2; 1; 3)	(6; 4; 7)	(8; 2; 7)	(4; 3; 4)
	(1; 5; 2)	(-1; 8; 4)	(-3; 2; 4)	(7; -1;-1)
	(6; 1; 4)	(2; 9; 5)	(3; 5; 5)	(12; 7; 1)
	(6; 5; 1)	(4; 7; 4)	(11; -3; -2)	(7; 3;-1)
	(3; 1; 5)	(7; 4; 9)	(8; 3; 9)	(7; 5; 7)
	(3; 2; 6)	(5; 5; 8)	(7; -1; 8)	(9; 8; 9)

 

Задание №4

 

Дано: a= l p + m q, b= n p - k q, угол между векторами p и q равен p/ f.

Значения коэффициентов l, m, n, k, f и модули векторов p и q даны ниже для каждого варианта.

Вычислить:

1) длины диагоналей параллелограмма, построенного на векторах а и в;

2) угол между диагоналями;

3) площадь параллелограмма.

Вариант	| p|	| q|	l	m	n	k	F
Вариант	| p |	| q |	l	m	n	k	F

 

Задание №5

 

Решить следующие задачи.

1. Написать уравнение эллипса, проходящего через точку пересечения гиперболы х ²- у ²=2 с прямой х+у -2=0, если известно, что фокусы эллипса совпадают с фокусами гиперболы.

2. Составить уравнение гиперболы, имеющие общие фокусы с эллипсом 24 х ²+49 у ²=1176 при условии, что ее эксцентриситет e=1,25.

3. Написать уравнение окружности такой, чтобы ее диаметром оказался отрезок прямой х+у -4=0, заключенный между осями координат.

4. Большая ось эллипса втрое больше его малой оси. Составить каноническое уравнение этого эллипса, если он проходит через точку М(3; ).

5. Дана гипербола х ²- у ²=8. Составить уравнение эллипса, проходящего через точку М(4;6) и имеющего фокусы, которые совпадают с фокусами данной гиперболы.

6. Найти точки пересечения параболы у ²=8 х с эллипсом, у которого правый фокус совпадает с фокусом этой параболы, большая полуось равна 4 и фокусы лежат на оси Ох.

7. Фокусы гиперболы лежат в точках F₁(;0) и F₂(;0). Гипербола проходит через точку А(2;0). Найти уравнение ее асимптот.

8. Найти параметр р параболы у ²=2 рх, если известно, что эта парабола проходит через точки пересечения прямой у=х с окружностью х ²+ у ²-6 х =0.

9. Найти точки пересечения параболы у ²= х с прямой, проходящей через фокус этой параболы параллельно ее директрисе.

10. Через правый фокус гиперболы 4 х ²-5 у ²=20 проведены прямые, параллельные ее асимптотам. Определить точки пересечения этих прямых с гиперболой.

11. Написать уравнение окружности такой, чтобы ее центр совпадал с фокусом параболы у ²=8 х и чтобы окружность прошла через начало координат.

12. Оси гиперболы совпадают с осями координат. Гипербола проходит через точки параболы х ²=2 у с прямой х -2 у +6=0. Составить уравнение этой гиперболы.

13. Эллипс проходит через точку пересечения прямой 3 х +2 у =7 с параболой у ²=4 х (взять точку с меньшей абсциссой). Оси эллипса совпадают с осями координат. Составить уравнение этого эллипса, если его эксцентриситет равен 0,6.

14. Эксцентриситет гиперболы в 2 раза больше углового коэффициента ее асимптоты. Гипербола проходит через точку М(3;-1), ее действительная ось лежит на оси Ох, а центр в начале координат. Найти точки пересечения этой гиперболы с окружностью х ²+ у ²=10.

15. Написать уравнение параболы, вершина которой находится в начале координат, а осью симметрии является ось Ох, если известно, что расстояние от ее фокуса до центра окружности х ²+ у ²-10 х -8 у +25=0 равно 5.

16. Составить каноническое уравнение эллипса, правая вершина которого совпадает с правым фокусом гиперболы 8 х ²- у ²=8. Эллипс проходит через точки пересечения параболы у ²=12 х с данной гиперболой.

17. Вычислить расстояние от фокуса гиперболы 4 х ²-5 у ²=20 до ее асимптот. Найти эксцентриситет этой гиперболы.

18. Найти точки пересечения параболы у ²= х с окружностью, которая проходит через начало координат, имеет центр на оси Ох и радиус, равный 5.

19. Составить уравнение эллипса, если его фокусы совпадают с фокусами гиперболы 4 х ²-5 у ²=20, аэксцентриситет эллипса равен 0,6.

20. Окружность имеет центр в левой вершине гиперболы х ²-4 у ²=16 и радиус, равный вещественной полуоси этой гиперболы. Найти точки пересечения этой окружности с асимптотами данной гиперболы.

21. Составить уравнение гиперболы, имеющей эксцентриситет e=1,5, если известно, что ее фокусы совпадают с фокусами эллипса 2 х ²+5 у ²=30.

22. Составить уравнение окружности, диаметром которой служит отрезок прямой х+у -4=0, вырезанный параболой у ²=2 х.

23. Найти расстояние от фокуса параболы 8 у = х ² до прямой 3 х +4 у +2=0.

24. Написать уравнение окружности, проходящей через точки А(3;0) и В(-1;2), если известно, что ее центр лежит на прямой х-у +2=0.

25. Вычислить расстояние от центра окружности х ²+ у ²=10 х до асимптот гиперболы х ²-4 у ²=20.

26. Составить каноническое уравнение эллипса, сумма полуосей которого равна 8 и расстояние между фокусами равно 8.

27. В эллипс 24 х ²+49 у ²=1176 вписан прямоугольник, две противоположные стороны которого проходят через фокусы. Вычислить площадь этого прямоугольника.

28. Составить уравнение окружности, проходящей через точки А(5;0) и В(1;4), если центр ее лежит на прямой х+у =3.

29. Написать каноническое уравнение эллипса, у которого эксцентриситет равен 0,8, а большая полуось больше малой полуоси на 2 единицы.

30. Найти каноническое уравнение гиперболы, проходящей через точку М(;2) и имеющей асимптоты 3 у =± х.

31. В эллипс х ²+4 у ²=4 вписан прямоугольник, площадь которого равна 4. Написать уравнения диагоналей этого прямоугольника.

32. Через фокус параболы у ²=4 х под острым углом к оси Ох проведена прямая. Написать уравнение этой прямой, если длина образовавшейся хорды равна 4,5.

 

Задание №6

 

Даны: координаты вершин пирамиды А₁ А₂ А₃ А_4.

Найти: 1) уравнение плоскости А₁ А₂А₃;

2) уравнения прямой А₁ А₂;

3) уравнения высоты, опущенной из вершины А₄ на грань А₁ А₂ А₃;

4) угол между ребром А₁ А₄ и гранью А, А₂ А₃.

 

 

Вариант	А1	А2	А3	А4
	(2; 3; 2)	(10; 7; 3)	(6; 6; 3)	(8; 9; 5)
	(3; 5; 2)	(1; 7; 5)	(5; 6; 8)	(1; 6; 4)
	(6; 1; 4)	(3;-3; 8)	(5;-5; 8)	(8; 3; 3)
	(2; 5; 4)	(5; 3; 6)	(8; 3; 5)	(8; 2; 10)
	(3; 4; 3)	(7;-4; 4)	(6; 0; 4)	(9; 10; 6)
	(1; 2; 3)	(3; 4; 6)	(-3; 1; 6)	(3; 3; 5)
	(3; 5; 1)	(0; 1; 5)	(1; 0; 5)	(7; 9; -1)
	(5;-2; 4)	(7; 1; 6)	(7; 4; 5)	(8; 4; 10)
	(1; 2; 1)	(9;-2; 2)	(-3; 5; 0)	(7; 8;-2)
	(4; 1; 3)	(2; 3; 6)	(5;-3; 6)	(3; 3; 5)
	(3;-1; 2)	(7; 2; 6)	(9; 0; 6)	(5; 1; 3)
	(3; 5; 4)	(1; 8; 6)	(-1; 2; 6)	(9;-1; 1)
	(1; 1; 2)	(-3;9; 3)	(-2; 5; 3)	(7; 7; -1)
	(1; 4; 3)	(-1; 6; 6)	(6; -4; 0)	(2; 2; 1)
	(2; 4; 1)	(6; 7; 5)	(7; 6; 5)	(6; 8; 3)
	(1; 2; 2)	(3; 5; 4)	(5;-1; 4)	(7; 8; 5)
	(2;-2; 1)	(10; 2; 2)	(6; 1; 2)	(8; 4; 4)
	(3; 4;-1)	(1; 6; 2)	(5; 5; 5)	(1; 5; 1)
	(2; 5; 3)	(-1; 1; 7)	(1; -1; 7)	(4; 7; 2)
Вариант	А1	А2	А3	А4
	(1; 4; 2)	(4; 2; 4)	(7; 2; 3)	(7; 1; 8)
	(3; 1; 4)	(7; -7; 5;)	(6; -3; 5)	(9; 7; 7)
	(2; 4; 3)	(4; 6; 6)	(-2; 3; 6)	(4; 5; 5)
	(5;-2;-1)	(2; -6; 3)	(3; -7; 3)	(9; 2; -3)
	(5; 2; 1)	(7; 5; 3)	(7; 8; 2)	(8; 8; 7)
	(2;-1; 7)	(10;-5; 8)	(-2; 2; 6)	(8; 5; 4)
	(4; 7; 8)	(2; 9; 11)	(5; 3; 11)	(3; 9; 10)
	(2; 1; 3)	(6; 4; 7)	(8; 2; 7)	(4; 3; 4)
	(1; 5; 2)	(-1; 8; 4)	(-3; 2; 4)	(7; -1;-1)
	(6; 1; 4)	(2; 9; 5)	(3; 5; 5)	(12; 7; 1)
	(6; 5; 1)	(4; 7; 4)	(11; -3; -2)	(7; 3;-1)
	(3; 1; 5)	(7; 4; 9)	(8; 3; 9)	(7; 5; 7)
	(3; 2; 6)	(5; 5; 8)	(7; -1; 8)	(9; 8; 9)

 

Задание №7

Найти точки разрыва функции, если они существуют, и построить ее график.

 

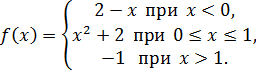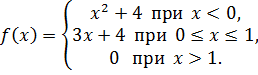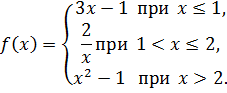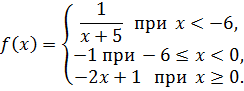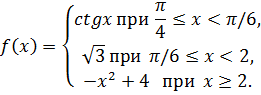Задание №8

 

Исследовать функцию и построить график.

 

	y = ex (2x2-5x+4)		y =
	y = (lnx-2)		y = 1- +arctg2x
	y = (3,3 +0,2x-0,3x2)		y = ln(x2-x+1)
	y =		y = ex(2x2+x+1)
	y = -1-arctg(x/2)		y = x3(3lnx-1)
	y = 2x2+5x+ln½x½		y= (3,8+1,3x-0,3x2)
	y = e-x(2x2+3x+2)		y = 2ln(x2+1)-3arctgx
	y = x3/2(lnx- )		y = 0,3x-1-arctg3x
	y = (2,8+0,8x-0,3x2)		y = (x2-5)
	y =		y = ln(x2+9)- arctg
	y = 1- +arctg(x/3)		y = x1/3
	y = 8x2+10x+ln½x½		y = 16x-arcsin2x
	y =xln(x2+ )-2x+ arctg		y = ln(x2-4x+13)
	y = e-x(2x2+9x+11)		y =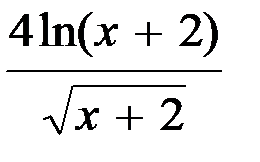
	y = x2(2lnx-1)		y =
	y = (1,7+1,4x-0,3x2)		y =

 

ПРИМЕР ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ №1

1. Даны точки: А(4;2;5) В(0;7;1) С(0;2;7) D(1;5;0).а) построить пирамиду АВСD; б) V_ABCD-?; в) S_DABC-?; г) cos(AB^ÙAC)?;

д) пр_ADAC-?.

2. Решить систему алгебраических уравнений:

 

3. Написать уравнение прямой, проходящей через правый фокус эллипс 16х²+25у²=400 и точку А(2;3). Найти площадь параллелограмма, построенного на векторах.

4. Написать уравнение плоскости, проходящей через прямую параллельно прямой .