Тригонометрическая форма комплексного числа

Например. Представить комплексное число в тригонометрической форме.

Решение: здесь , найдем

, точка с координатами находится в 4 четверти координатной плоскости, , следовательно , данное число в тригонометрической форме будет иметь вид:

Действия над комплексными числами, заданными в тригонометрической форме.

Формула Муавра.

Эта формула позволяет возводить в степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

Аналогичная формула применима также и при вычислении корней n -ой степени из ненулевого комплексного числа:

Показательная форма комплексного числа:

Тригонометрическую форму комплексного числа можно заменить показательной:

Пример.

Представить число в тригонометрической и показательной форме.

Решение. , b=-1, r=

,

И следовательно 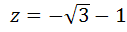=2 ;

В показательной форме: