Тригонометрический ряд Фурье

Опр.1 Ряд вида 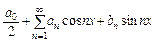(1) называется тригонометрическим рядом. Его частичные суммы явл-ся лин. комбинациями ф-й, входящих в систему

cos x, sin x, cos 2x, sin 2x, …, cos nx, sin nx, …. (2)

Опр.2 Множество ф-ий (2) наз-ся тригонометрической системой.

Лемма 1. Тригонометрическая система (2) обладает свойствами:

ортогональность, т.е. интеграл по отрезку [-π, π] от произведения двух

различных функций, входящих в нее, равен нулю

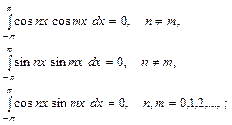(3)

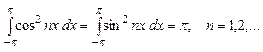2) (4)

Теорема 1. Пусть 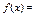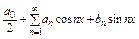(5) и ряд, стоящий в правой части этого равенства, сходится равномерно на отрезке [-π, π]. Тогда

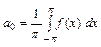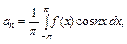
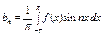, , n =1,2, …. (6)

Опр.3 Пусть функция f абсолютно интегрируема на отрезке [-π, π]. Тригонометрический ряд (1), коэффициенты которого задаются формулами (6), называется тригонометрическим рядом Фурье, а числа a_n и b_n – коэффициентами Фурье функции f.

Теорему 1 в этих терминах можно перефразировать следующим образом:

всякий равномерно сходящийся тригонометрический ряд является рядом Фурье своей суммы.

Разложение функции в тригонометрический ряд Фурье единственно

Функция 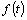, 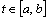называется кусочно-гладкой на 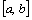, если как сама функция 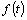, так и ее производная функция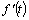
непрерывны или кусочно-непрерывны на .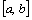

ТЕОРЕМА (о достаточных условиях сходимости ТРФ)

Если 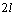–периодическая функция 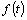кусочно-гладкая на 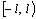, то
1) ТРФ функции 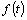существует; 2) ТРФ сходится всюду;
3) сумма ТРФ равна 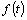в каждой точке непрерывности функции 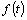и равна числу 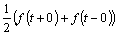– (полусумме значений лево- и правостороннего пределов функции 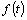) в каждой ее точке разрыва.