Основные формулы тригонометрии
Перевод градусной меры угла в радианную и обратно. Пусть a° - градусная мера угла, b - радианная, тогда справедливы формулы:
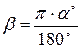
| 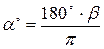
|
Формулы зависимости между функциями одного и того же аргумента.
| 1. | 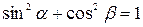
| 4. | 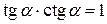
|
| 2. | 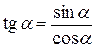
| 5. | 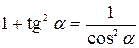
|
| 3. | 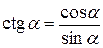
| 6. | 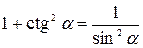
|
Формулы сложения.
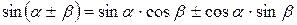
|
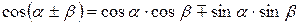
|
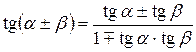
|
Формулы двойных и половинных углов.
| 1. | 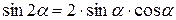
| 5. | 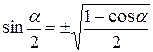
|
| 2. | 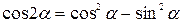
| 6. | 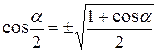
|
| 3. | 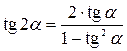
| 7. | 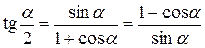
|
| 4. | 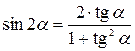
| 8. | 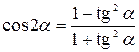
|
Формулы преобразования суммы в произведение.
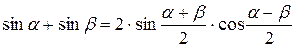
|
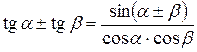
|
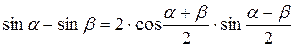
| |
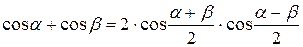
| 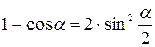
|
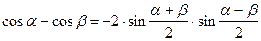
| 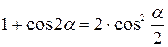
|
Формулы преобразования произведения в сумму.
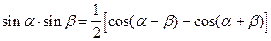
|
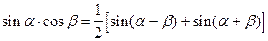
|
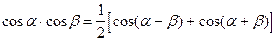
|
Формулы приведения.
| j | 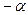
| 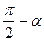
| 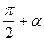
| 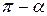
| 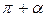
| 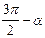
| 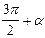
| 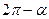
| 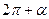
|
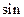 j j
| - 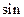 a a
| 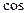 a a
| 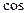 a a
| 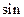 a a
| - 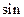 a a
| - 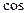 a a
| - 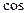 a a
| - 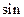 a a
| 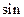 a a
|
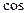 j j
| 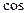 a a
| 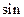 a a
| - 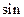 a a
| - 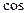 a a
| - 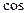 a a
| - 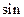 a a
| 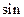 a a
| 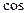 a a
| 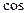 a a
|
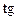 j j
| - 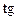 a a
| 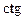 a a
| - 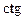 a a
| - 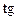 a a
| 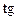 a a
| 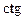 a a
| - 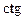 a a
| - 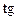 a a
| 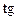 a a
|
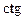 j j
| - 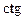 a a
| 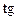 a a
| - 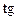 a a
| - 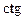 a a
| 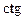 a a
| 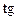 a a
| - 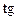 a a
| - 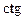 a a
| 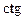 a a
|
Решение простейших тригонометрических уравнений
| Уравнение | Общее решение | Частные случаи | ||
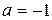
| 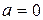
| 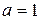
| ||
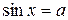 , ,
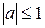
| 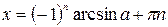
| 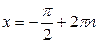
|
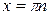
| 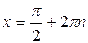
|
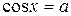 , ,
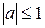
| 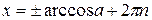
|
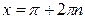
| 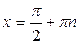
|
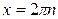
|
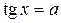 , ,
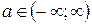
| 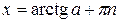
| 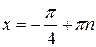
|
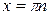
| 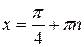
|
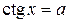 , ,
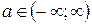
| 
| 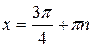
| 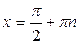
| 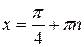
|
Для решения простейших тригонометрических неравенств 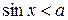 ,
, 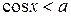 ,
, 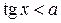 ,
, 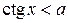 (вместо знака
(вместо знака 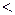 могут стоять
могут стоять 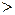 ,
, 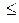 ,
, 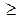 ) применяют графический способ. Находят точки пересечения графика соответствующей функции с прямой
) применяют графический способ. Находят точки пересечения графика соответствующей функции с прямой 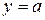 , расположенные ближе к началу координат, и затем используют периодичность функции.
, расположенные ближе к началу координат, и затем используют периодичность функции.
Для решения более сложных тригонометрических неравенств их сводят к простейшим случаям с помощью упрощений.
Графики и основные свойства тригонометрических функций.
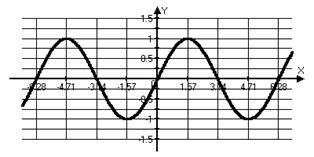
| 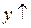 для для 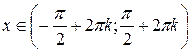
|
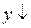 для для 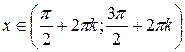
| |
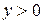 для для 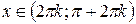
| |
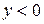 для для 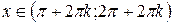
| |
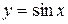 , , 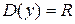 , , 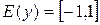 , период , период 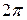 , нечетная , нечетная
| |
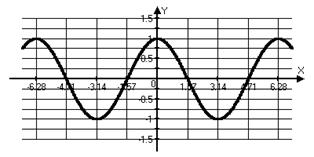
| 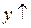 для для 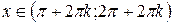
|
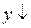 для для 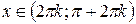
| |
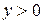 для для 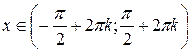
| |
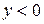 для для 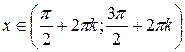
| |
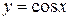 , , 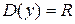 , , 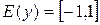 , период , период 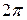 , четная , четная
| |
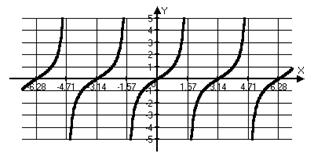
| 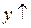 для для 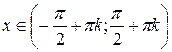
|
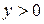 для для 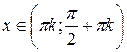
| |
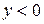 для для 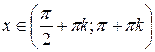
| |
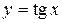 , , 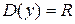 \ \ 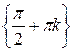 , , 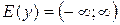 , период , период 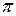 , нечетная , нечетная
| |
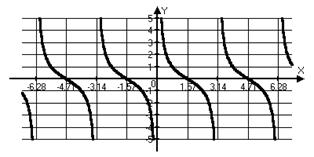
| 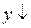 для для 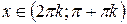
|
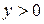 для для 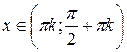
| |
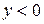 для для 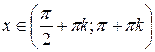
| |
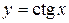 , , 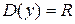 \ \ 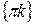 , , 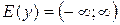 , период , период 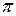 , нечетная , нечетная
|
Графики и основные свойства обратных тригонометрических функций.
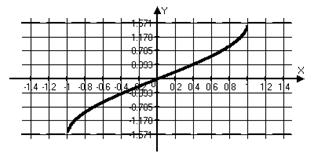
| 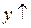 для для 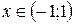
|
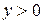 для для 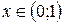
| |
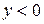 для для 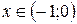
| |
| Функция нечетная | |
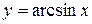 , , 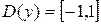 , , 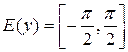 , непериодическая функция , непериодическая функция
| |
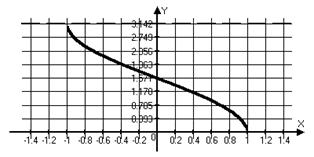
| 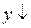 для для 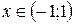
|
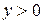 для для 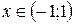
| |
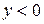 для для 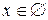
| |
| Функция ни четная, ни нечетная | |
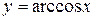 , , 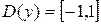 , , 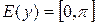 , непериодическая функция , непериодическая функция
| |
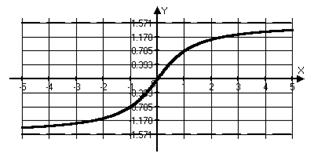
| 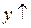 для для 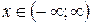
|
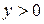 для для 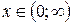
| |
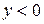 для для 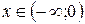
| |
| Функция нечетная | |
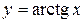 , , 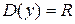 , , 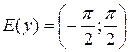 , непериодическая функция , непериодическая функция
| |
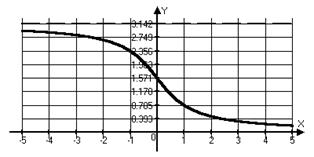
| 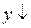 для для 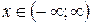
|
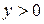 для для 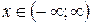
| |
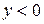 для для 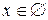
| |
| Функция ни четная, ни нечетная | |
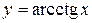 , , 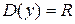 , , 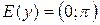 , непериодическая функция , непериодическая функция
|
Связь тригонометрических функций с обратными тригонометрическими функциями осуществляется при помощи следующей таблицы
| 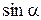
| 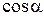
| 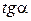
| 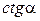
|
-90°= 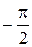
| -1 | - | -¥ | - |
-60°= 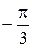
| - 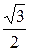
| - | - 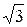
| - |
-45°= 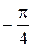
| - 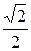
| - | -1 | - |
-30°= 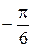
| - 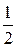
| - | - 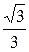
| - |
| ¥ | ||||
30°= 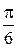
| 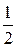
| 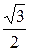
| 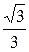
| 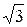
|
45°= 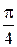
| 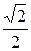
| 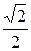
| ||
60°= 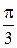
| 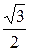
| 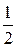
| 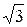
| 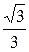
|
90°= 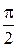
| ¥ | |||
120°= 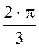
| - | - 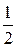
| - | - 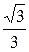
|
135°= 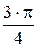
| - | - 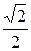
| - | - 1 |
150°= 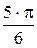
| - | - 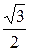
| - | - 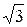
|
180°= 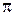
| - | -1 | - | - ¥ |
 2015-01-21
2015-01-21 575
575








