2017-11-01
1647
Стоимость облигации как актива оценить гораздо легче, чем, например, акции. Облигация имеет конечный срок погашения, поток платежей (купонных выплат) в большинстве случаев фиксирован (в отличие от дивидендов по акции). Здесь существенно меньше факторов риска и неопределенности, чем в случае акций.
Виды стоимости облигации:
· номинальная
· «чистая»
· «грязная»
При выпуске облигации размещаются, как правило, по номиналу или с небольшим отклонением от номинала – с дисконтом или с премией (только дисконтные облигации, по которым не выплачивается процентный доход, всегда размещаются по цене ниже номинала).
Однако в дальнейшем их цена может весьма заметно отклоняться от номинала. Возьмем для примера классическую купонную облигацию. Какие факторы лежат в основе динамики ее цены?
Основной фактор – это соотношение рыночной, т.е. текущей, процентной ставки и купонной ставки по облигации.
25-летняя облигация выпущена в 1990 году в период относительно высоких процентных ставок на мировом рынке. Значит, чтобы ее купили, эмитенту необходимо было установить по ней также высокую купонную ставку. Предположим, что облигация размещалась по номиналу $1000 с купонной ставкой в 10%. К 2012 году процентные ставки на рынке упали. Облигации эмитентов с аналогичным рейтингом (т.е. с таким же уровнем риска) выпускаются со ставкой 4% годовых. Если наш инвестор, имевший старую облигацию, захочет ее продать, он сможет это сделать не за $1000, а за бóльшую цену – такую, которая обеспечит примерную доходность в размере 4%. Если рынок обнаруживает инструменты, обеспечивающие более высокую доходность, чем другие, то все начинают покупать этот инструмент, благодаря чему происходит выравнивание цен.
| Общее правило: при росте рыночных процентных ставок цена облигации с фиксированной купонной ставкой падает, при падении – повышается. |
| Текущая (чистая) рыночная стоимость облигации – сумма дисконтированных денежных потоков в первый день купонного периода. |
 ,
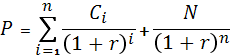где Р – чистая цена облигации;
С – величина купонного платежа;
r – требуемая норма доходности (она же – доходность до погашения) в виде десятичной дроби;
N – номинал облигации;
n – число периодов начисления (количество лет до погашения).
|
Зависимость цены облигации от купонной ставки, срока до погашения облигации и текущей рыночной процентной ставкой описывается формулой, опирающейся на формулу дисконтирования по сложным процентам.
Вставка
В предыдущем примере найдем цену этой облигации, если до ее погашения остается еще три года.
Р = 100/1,04 + 100/1,08 + (100 + 1000)/1,125 = $1166,52.
В некоторых случаях формула чистой цены требует уточнения.
1. Купон выплачивается несколько раз в год. Как уже указывалось, ставка купона по облигации объявляется в годовых процентах. В случае, если купон выплачивается несколько раз в год, ставка делится на количество выплат. Например, купон 10% выплачивается два раза в год. Это означает, что каждые полгода эмитент выплачивает по 5% от номинала облигации. В этом случае при оценке чистой стоимости облигации необходимо дисконтировать каждый платеж. Но при этом необходимо учитывать, что ставка дисконтирования (рыночной доходности), которая находится в знаменателе формулы, тоже указана в годовых процентах, поэтому ее также необходимо делить на количество выплат купона в год.
Таким образом, формула преобразуется:
,
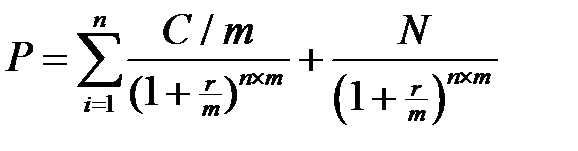где Р – цена облигации;
С – величина купонного платежа;
r – требуемая норма доходности в виде десятичной дроби;
N – номинал облигации;
n – количество лет до погашения;
m – количество выплат в год.
