Расчеты на прочность и жесткость

ПРИ ПРЯМОМ ИЗГИБЕ

 

Схема нагружения.

Прямой изгиб – это такой вид нагружения, при котором нагрузки действуют в одной главной плоскости бруса перпендикулярно к его продольной оси. Стержни, работающие на изгиб, называют балками.

Внутренние усилия.

В поперечном сечении балок возникают два внутренних усилия: поперечная (перерезывающая) сила Q _z и изгибающий момент M _y.

Из уравнений равновесия для отсеченных частей (10,3) по методу сечений следует, что поперечная (перерезывающая) сила Q _z в произвольном поперечном сечении численно равна алгебраической сумме проекций на поперечную ось z сечения (являющуюся силовой линией) всех внешних сил, приложенных по одну сторону от рассматриваемого сечения. Для нее справедливо выражение

q _z (x) = dQ _z (x)/dx = tg α _Q, (31)

где q _z (x) – интенсивностью внешней поперечной силы,

α _Q – угол между касательной к эпюре Q и осью абсцисс x.

Из метода сечений (10,5) так же следует, что в произвольном поперечном сечении балки изгибающий момент M _y численно равен алгебраической сумме моментов всех внешних усилий, приложенных по одну сторону от рассматриваемого сечения, взятых относительно центра массы сечения. Для изгибающего момента справедливо выражение

Q _z (x) = dM _y (x)/dx = tg α _M, (32)

где α _M – угол между касательной к эпюре M _y и осью абсцисс x.

Из выражений (31) и (32) следуют правила для проверки соответствия эпюр поперечной силы и изгибающего момента расчетной схеме:

1. Если на участке отсутствует распределенная нагрузка, то поперечная сила постоянна, а изгибающий момент изменяется по линейному закону (на эпюре будет наклонная прямая).

2. Если на участке действует равномерно распределенная нагрузка, то поперечная сила меняется по линейному закону, а изгибающий момент – по закону квадратичной параболы. При этом парабола всегда обращена выпуклостью навстречу распределенной нагрузке.

3. В сечении, где приложена внешняя сосредоточенная сила, эпюра Q имеет скачок на величину этой силы, а эпюра М – излом.

4. В сечении, где приложен внешний сосредоточенный момент, эпюра М имеет скачок на величину этого момента. На эпюре Q это не отражается.

5. В торцевом сечении балки поперечная сила и изгибающий момент равны соответственно приложенным в этом сечении внешней сосредоточенной силе (активной или реактивной) и моменту сосредоточенной пары (активной или реактивной).

6. Если внешние силы направлены вниз, то при увеличении абсциссы х (начало отсчета слева) поперечная силаубывает. Если поперечная сила положительна, то при увеличении абсциссы х изгибающий момент возрастает.

7. В сечении, где поперечная сила переходит через ноль, изгибающий момент достигает экстремального значения.

8. Эпюры должны выходить из нуля и уходить в нуль (вне твердого тела внутреннего усилия нет).

Совместное построение эпюр позволяет лучше контролировать правильность их расчета. Опасное сечение находится по эпюре изгибающих моментов, так как он является при изгибе более опасным с точки зрения прочности внутренним усилием.

Напряжения.

Расчет на прочность при прямом изгибе основан на анализе работы опасного сечения конструкции. В общем случае (рис. 8) часть волокон бруса находится в растянутом состоянии, а другая (со стороны центра кривизны) в сжатом. Срединный слой (по оси х) не удлиняется и называется нейтральным слоем. В поперечном сечении ему соответствует нейтральная линия. Максимальные нормальные напряжения возникают в наиболее удаленных от нейтральной линии точках сечения. Считая, что в общем случае прямого изгиба (Q _z ≠ 0) расчетное соотношение для нормальных напряжений совпадает с соответствующим выражением для случая чистого изгиба (Q _z (x) = 0, M _y (x) = const), на основании гипотезы плоских сечений получим:

(33)

 

Рис. 8: Эпюра нормальных напряжений в поперечном сечении при прямом (чистом) изгибе

 

Здесь J _y, мм⁴ – осевой момент инерции поперечного сече-

ния балки относительно нейтральной линии, которая совпадает с главной центральной осью инерции сечения y, z _mах – координата точки (точек) сечения, наиболее удаленной от нейтральной линии.

Формула записана в прямоугольной (декартовой) системе координат, в которой осями являются главные центральные оси инерции сечения. Частным случаем этих осей являются оси симметрии. Распределение нормальных напряжений по высоте сечения относительно нейтральной линии, представленное соотношением (33), не зависит от конфигурации сечения.

В сечениях, симметричных относительно оси у, │z _max │= =│z _min │, и условие прочности при прямом изгибе получает вид

. (34)

Здесь W_y = J_y/ │z _max │ _, мм³ – осевой момент сопротивления сечения балки относительно нейтральной линии.

Для пластичных материалов, имеющих равные допускаемые напряжения на растяжение и сжатие, экономичной формой поперечного сечения балки, с точки зрения уменьшения расхода материала, является форма симметричная относительно нейтральной линии. Это профиль типа стандартного двутавра, швеллера и их комбинации с обязательной ориентацией нагрузки вдоль стенки профилей. Ориентация нагрузки параллельно полкам профилей нецелесообразна вследствие резкого снижения прочности и увеличения податливости.

При расчете балок, состоящих из двух и более одинаковых профилей поставленных рядом вдоль нейтральной линии, их моменты инерции и моменты сопротивления складываются.

Вместе с тем следует отметить, что более точный расчет на прочность при изгибе тонкостенных конструкций необходимо проводить по главным напряжениям [1-3], то есть с учетом касательных напряжений, которые обусловлены поперечной силой Q _z. Надо иметь в виду, что опасные сечения по моменту и поперечной силе могут не совпадать.

Перемещения.

При изгибе балок учитываются два перемещения поперечных сечений: прогиб z – перемещение центра масс сечения по нормали к недеформированной продольной оси и угол поворота сечения q вокруг поперечной оси, совпадающей с нейт-ральной линией. Соответственно могут использоваться два условия жесткости балочных конструкций:

z _max £ [ z ] (мм); (35)

q _max £ [ q ] (рад). (36)

Здесь z _max, q _max – максимальные значения прогиба балки и угла поворота; [ z ], [ q ] – допускаемые значения, которые зависят только от назначения балочных конструкций, а не от материала.Обычно z _max ⁄ l £ 1 ⁄ 250 ¸ 1 ⁄ 500; q _max £ 0,0001 (рад), где l – длина пролета или консоли.

Для определения перемещений при изгибе используется дифференциальное уравнение изогнутой оси балки в виде

(37)

где ЕJ _y – жесткость поперечного сечения балки при изгибе, Е – модуль продольной упругости, J _y – осевой момент инерции поперечного сечения балки относительно нейтральной линии, z ”(x) – кривизна балки (величина обратная радиусу кривизны r), М _y (х) – внутренний изгибающий момент.

Последовательное интегрирование уравнения (37) приводит соответственно к уравнениям для определения углов поворота сечений 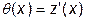и прогибов z (x).

, (38)

. (39)

Здесь C, D –постоянные интегрирования. Их физический смысл: С – угол поворота, а D – прогиб балки в начале координат в масштабе жесткости ЕJ _y, то есть C=EJ _y q (0) и D=EJ _y z (0). Постоянные интегрирования определяются из граничных условий (условий опирания балок). Для этого выявляются такие сечения балки, где обращается в нуль прогиб или угол поворота. Равенство нулю перемещений, то есть их запрещение, означает наложение на конструкцию связей с появлением соответствующих реакций связей. Так, для наиболее характерных расчетных схем граничными условиями являются: равенство нулю угла поворота и прогиба в сечении жесткого защемления у консольных балок (рис.9) или прогибов на обеих опорах у двухопорных балок (рис.10).

Эти три уравнения (37 – 39) образуют алгоритм аналитического метода определения перемещений.

Для балок, имеющих несколько участков, с целью упрощения вычислительных процедур, в уравнение (37) подставляется выражение внутреннего изгибающего момента для последнего участка (от базового начала координат). При его составлении необходимо выполнить следующие условия:

1. Условно отсеченная часть включает базовое начало координат, которое располагается в крайней точке балки.

2. Все слагаемые моменты от внешних усилий должны иметь сомножитель типа , где l _i – расстояние от начала координат до соответствующего усилия, k – показатель степени, нормирующий размерность:

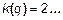
3. Для выполнения этого условия оканчивающаяся распределенная сила должна быть преобразована, то есть продолжена до конца балки, а вновь добавленная сила уравновешена равной встречной. Каждая из этих нагрузок (заданная – продолженная и уравновешивающая) описываются своим слагаемым.

4. Интегрирование уравнений проводится без раскрытия скобок.

Чтобы выражения изгибающего момента и перемещений можно было использовать для любого участка, вводят функциональный прерыватель (Н.Г. Бубнова), в качестве дискретного сомножителя . При выполнении условия при прерывателе член выражения используется (умножается на 1), а при невыполнении – не используется (умножается на 0). Записанные таким образом уравнения называют универсальными, так как они справедливы для любого участка.

Изложенный метод является разновидностью метода начальных параметров, в котором запись ведется без применения прерывателей.

 

Пример 3.

Для заданной консольной балки (рис.9а), нагруженной сосредоточенными силами, выполнить расчет на прочность и жесткость.

1. Реактивные усилия.

Реакции связей, то есть реактивная сила и реактивный момент, вычисляются из двух уравнений равновесия: суммы проекций сил на вертикальную ось и суммы моментов относительно точки заделки:

∑ P _iz = R – P – P = 0; → R = 2 P;

∑ M ₀ = M _R – P×l – P× 2 l = 0; → M _R = 3P×l.

4. Внутренние усилия.

При построении эпюр внутренних усилий достаточно анализа двух сечений балки (рис.9,а и 9,б).

Первый участок (сечение). Уравнения равновесия в следящей системе координат для левой части:

∑ P _iz = Q _z (x ₁) – R = 0; → Q _z (x ₁) = R = 2 P = const.

∑ M ₀ = M _y (x ₁) – R×x ₁ + M _R = 0; → M _y (x ₁) = R×x ₁ – M _R.

Границы изменения параметра x ₁ в пределах первого участка составляют 0 ≤ x ₁ ≤ l. После подстановки граничных значений в выражение для момента, получим

М _y (0) = - M _R = -ЗР×l; M _y (l) = -M _R + R×l = -3P×l + 2P×l = - P×l.

Второй участок (рис.9,б) 0 ≤ x ₂ ≤ l.

Начало следящей системы координат размещается на свободном краю консоли. Соответствующие уравнения для правой части имеют вид

∑ P _iz = Q _z (x ₂ ) – P = 0; → Q _z (x ₂ ) = P = const;

∑ M ₀ = M _y (x ₂) + P ×x ₂ = 0; → M _y (x ₂) = - P×x ₂ ; М _y (0)=0; М _y (l)=-Р∙l.

Эпюры поперечных сил и изгибающих моментов для рассматриваемой расчетной схемы приведены на рис.9,в и 9,г.

При изгибе более опасным внутренним усилием с точки зрения прочности является изгибающий момент. Таким образом, опасным в этой консольной балке является сечение жесткой связи, в котором │ M _max │=3 Pl.

3. Условие прочности.

Для рассматриваемого примера эпюра максимальных нормальных напряжений качественно повторяет эпюру моментов M _y (рис.9,г), так как балка имеет постоянное по длине сечение. Условие прочности проверяется для опасного сечения, которое находится в заделке.

.

 

Рис. 9. Прямой изгиб (к примеру 3):

а – расчетная схема; б – рассматриваемые отсеченные части;

в – эпюра поперечных сил; г – эпюра изгибающих моментов;

д – эпюра прогибов

Решение условия прочности относительно внутреннего изгибающего момента приводит к определению допускаемой нагрузки. Для данной расчетной схемы это условие приобретает вид

Для расчета необходимого размера сечения вычисляется предварительно момент сопротивления

Подбор номера двутавра или швеллера проводится по таблицам соответствующих стандартов [1,2,3].

Для простых (нестандартных) профилей необходимые габариты сечения вычисляются с использованием следующих аналитических соотношений:

– для прямоугольного сечения (рис. 8) со сторонами b ´ h (для этого профиля большую роль играет размер вдоль силы)

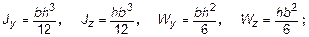
– для круглого сечения

– для кольцевого сечения (труба)

В качестве примера рационального подхода при проектировании конструкции положим в рассматриваемом примере (рис.9) Р =5 кН, l =1м, [ σ ]=160 МПа.

Для определения необходимого момента сопротивления используем условие прочности (34)

Обращаясь к справочным таблицам и принимая во внимание ориентацию осей, определяем необходимый номер двутавра – № 16 с моментом сопротивления W _y = 109 см ³.

Действительная величина напряжений при использовании этого профиля составляет

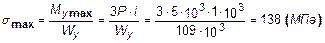
То есть условие прочности выполняется.

Проверим возможность применения двутавра меньшего номера – №14 с моментом сопротивления W _y =81,7 см ³.

Таким образом, величина перегрузки превышает допустимые 5%.

Ориентация нагрузки параллельно полкам профиля нецелесообразна вследствие резкого увеличения податливости и снижения прочности. Так, в рассматриваемом примере необходимым номером двутавра в горизонтальном положении будет лишь №45 с W _z = 101 см ³. При эквивалентной прочности последняя конструкция неэкономична и оказывается в 4,2 раза тяжелее.

4. Перемещения.

Для этой балки (рис.9) уравнение (37) получает вид

. (40)

Ограничитель x ≥ l определяет зону действия слагаемого, он аналогичен сомножителю Δ: при x < l Δ=0; при x > l Δ=1.

Последовательное интегрирование этого уравнения приводит соответственно к уравнениям для определения углов поворота сечений 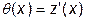и прогибов z (x). Интегрирование уравнения проводится без раскрытия скобок:

(41)

(42)

Находим постоянные интегрирования C,D из граничных условий. В защемлении при х = 0 z' (0) = φ (0) = 0, что означает отсутствие поворота сечения балки в месте жесткой связи и физически связано с появлением реактивного момента M _R. Подстановка условия в уравнение угла поворота (41) с учетом удаления третьего слагаемого (x = 0 < l) дает С =0. Там же при х = 0 z (0) = 0, что означает отсутствие прогиба сечения балки в месте жесткой связи и физически связано с появлением реактивной силы R. При подстановке условия в уравнение прогибов (42) с учетом удаления третьего слагаемого константа D =0. Равенство констант нулю соответствует их физическому смыслу как нулевому углу поворота (С) и нулевому прогибу (D) балки в начале координат в масштабе жесткости ЕJ _y.

Для расчета перемещения в заданном сечении в уравнения (41) или (42) подставляется соответствующее значение его координаты х. Так для расчета прогиба в сечении А (рис. 9,а) необходимо в уравнение (42) подставить x=2 l. В этом случае

Знак минус указывает, что в принятой базовой системе координат z-x балка прогибается вниз. Для построения эпюры перемещений (рис.9,б), в уравнение (42) вводятся последовательно значения параметра x.

 

Пример 4.

Для заданной балки (рис.10) построить эпюры изгибающих моментов и прогибов.

1. Реактивные усилия.

Уравнения равновемсия (моментов) относительно опор:

 

∑ ₂ M = P×l – q×l ² ⁄ 2 – M + R ₄ ×2l + q×l× 2,5l = 0; R ₄ = – 0,75q×l,

∑ ₄ M = P×3l – R ₂ ×2l + q×l× 1,5l – M + q×l ² / 2 = 0; R ₂ = 1,75q×l.

Проверка: ∑ P _z = 0; – P + R ₂ – q×l + R ₄ – q×l =0.

2. Внутренние усилия.

1 участок (левая часть балки): x Є [ 0; l ],

Q _z (x) = – P = – q×l/2 = const,

M _y (x) = – P×x (наклонная прямая), M _y (0) = 0; M _y (l) = – P×l = – q×l ² ⁄ 2.

2 участок (левая часть балки): x Є [ l; 2l ],

Q _z (x) = – P + R ₂ – q(x – l) (на эпюре наклонная прямая),

Q _z (l) = – P + R ₂ = 3q×l /4, Q _z (2l) = – P + R ₂ – q×l = – q×l /4.

M _y (x) = – P×x +R ₂ (x – l) – q(x – l) ² /2 ( парабола выпуклостью вверх),

M _y (l) = – P×l = – q×l ² /2, M _y (2l) = – P×2l +R ₂ l – q×l ² /2 = – q×l ² /4.

На этом участке Q _z (x) меняет знак, поэтому на эпюре M _y (x) имеется максимум:

Q _z (x _m ) = – P + R ₂ – q×(x _m – l) = 0, x _m = l+ ( – P + R ₂ )/q×= 7l /4,

M _{y max} = M _y (x _m ) = – 7q×l ² /32.

3 участок (левая часть балки): x Є [ 2l; 3l ]

Q _z (x) = – P + R ₂ – q×l = – ql /4 = const,

M _y (x) = – P×x +R ₂ (x – l) – q×l (x – 3l/2) +M (наклонная прямая).

С учетом преобразования распределенной силы (рис.10,б)

M _y (x) = – P×x +R ₂ (x – l) – q(x – l) ² /2 +M (x – 2l) ⁰ +q(x – 2l) ² /2,

M _y (2l) = – P2l +R ₂ l – q×l ² /2 +M =3q×l ² /4,

M _y (3l) = – P3l +R ₂ 2l – 3q×l ² /2 +M =q×l ² /2.

4 участок (левая часть балки): x Є [ 3l; 4l ],

Q _z (x) = – P + R ₂ – q×l +R ₄ + q×(x – 3l) (наклонная прямая),

Q _z (3l) = – P + R ₂ – q×l +R ₄ = – ql, Q _z (4l) = – P + R ₂ – q×l +R ₄ + q×l=0.

M _y (x) = – P×x +R ₂ (x – l) – q×l (x –3 l/2) +M+R ₄ (x – 3l) +q(x – 3l) ² /2

( парабола выпуклостью вниз).

С учетом преобразования распределенной силы (рис.10,б)

M _y (x) = – Px +R ₂ (x – l) – q(x – l) ² /2 +M (x – 2l) ⁰ +q(x – 2l) ² /2 +R ₄ (x – 3l)+

+q(x – 3l) ² /2,

M _y (3l) = –P3l +R ₂ 2l –3q×l ² /2 +M =q×l ² /2,

M _y (4l) = – P4l +R ₂ 3l – 5q×l ² /2 +M +R ₄ l+q×l ² /2 =0.

Опасным в балке является сечение посередине пролета справа от сосредоточенного момента (рис.10,г), где │ M _max │= = M _y (2l) = 3q×l ² /4.

3. Перемещения.

Универсальное дифференциальное уравнение изогнутой продольной оси балки

 

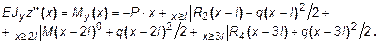
Универсальное уравнение углов поворота сечений

 

Универсальное уравнение прогибов

 

Используем граничные условия балки (условия на опорах):

z(x=l)=0, 0=D+C·l-P·l ³ /6;

z(x=3l)=0, 0=D+C·3l-P·(3l) ³ /6+ R ₂ (2l) ³ /6-q (2l) ⁴ /24+M·l ² /2+ q l ⁴ /24.

C=15q·l ³ /48=0,3125 q·l ³; D=-11q·l ⁴ /48=-0,2292 q·l ⁴ .

 

Расчет значений прогибов проведем в табличной форме.

 

x		0,5l	1,0l	1,5l	2,0l	2,5l	3,0l	3,5l	4,0l
D/(q·l 4 )	-0,2292	-0,2292	-0,2292	-0,2292	-0,2292	-0,2292	-0,2292	-0,2292	-0,2292
C·x/(q·l 4 )		0,1562	0,3125	0,4688	0,6250	0,7812	0,9375	1,0938	1,2500
-P·x 3 /(6q·l 4 )	—	-0,0104	-0,0833	-0,2815	-0,6667	-1,3021	-2,2500	-3,5729	-5,3333
+R 2 (x – l) 3 /(6q·l 4 )	—	—		0,0260	0,2083	0,7031	1,6667	3,2552	5,6250
– q(x – l) 4 /(24q·l 4 )	—	—		-0,0026	-0,0417	-0,2109	-0,6667	-1,6276	-3,3750
+M (x – 2l) 2 /(2q·l 4 )	—	—	—	—		0,1250	0,5000	1,1250	2,0000
+q(x – 2l) 4 /(24q·l 4 )	—	—	—	—		0,0026	0,0417	0,2109	0,6667
+R 4 (x – 3l) /(6q·l 4 )	—	—	—	—	—	—		-0,0156	-0,1250
+q(x – 3l) 4 /(24q·l 4 )	—	—	—	—	—	—		0,0026	0,0417
Σ = z·E·J/(q·l 4 )	-0,2292	-0,0104	0,0	-0,0185	-0,1047	-0,1303	0,0	0,2422	0,5209

Сравнение эпюр изгибающих моментов (рис.10,г), и прогибов (рис.10,д), позволяет проконтролировать правильность их построения. На участках, где изгибающий момент положителен, балка изгибается выпуклостью вниз.

 

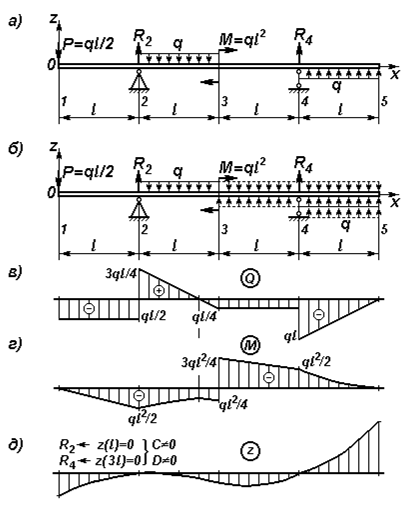
Рис. 10. Прямой изгиб (к примеру 4):

а – расчетная схема; б – расчетная схема с преобразованной распределенной силой; в – эпюра поперечных сил; г – эпюра изгибающих моментов; д – эпюра прогибов

 

 

Вопросы для самопроверки

 

1. Какой изгиб называют чистым, а какой – поперечным? 2. Какие балки называют статически определимыми? 3. Как определить изгибающий момент и поперечную силу в каком-либо сечении балки? 4. Какие допущения принимаются при изгибе? 5. Какая зависимость имеется между моментом и перерезывающей силой? 6. Как определить максимальный изгибающий момент? 7. Как распределены нормальные напряжения в поперечных сечениях балки? 8. Чему равны напряжения изгиба? 9. Что называется нейтральным слоем и где он расположен? 10. Что называется моментом инерции при изгибе? 11. В каких плоскостях возникают касательные напряжения при изгибе? 12. По какой формуле определяют величину касательных напряжений? 13. Как определить координаты центра тяжести плоской фигуры? 14. Чему равна сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей? 15. Какие оси называют главными? 16. Для каких фигур можно без вычислений определить положение главных центральных осей? 17. Относительно каких центральных осей осевые моменты инерции имеют наибольшее и наименьшее значения? 18. Что называется моментом сопротивления при изгибе? 19. Как выгоднее нагрузить балку прямоугольного сечения? 20. Как запишется дифференциальное уравнение изогнутой оси балки в общем виде? 21. Как найти постоянные интегрирования и что они обозначают? 22. Как найти наибольшее значение прогиба? 23. Какой случай изгиба называют косым изгибом? 24. В каких точках поперечного сечения возникают наибольшие напряжения при косом изгибе? 25. Как находят положение нейтральной линии при косом изгибе? 26. Как пройдет нейтральная линия, если плоскость действия сил совпадает с диагональной плоскостью балки прямоугольного поперечного сечения? 27. Как определяют деформации при косом изгибе? 28. Чему равно напряжение в центре тяжести поперечного сечения при внецентренном растяжении или сжатии? 29. Как находят напряжения в произвольной точке поперечного сечения при внецентренном растяжении или сжатии? 30. Какое положение занимает нейтральная линия, когда продольная сила приложена в вершине ядра сечения? 31. Какие напряжения возникают в поперечном сечении бруса при изгибе с кручением? 32. Как находят опасные сечения бруса при изгибе с кручением? 33. В каких точках круглого поперечного сечения возникают наибольшие напряжения при изгибе с кручением? 34. Как находится числовое значение расчетного момента при изгибе с кручением бруса круглого поперечного сечения?