Расчеты на прочность и жесткость

ПРИ ЦЕНТРАЛЬНОМ РАСТЯЖЕНИИ И СЖАТИИ

Схема нагружения.

Центральным растяжением или сжатием называют такой вид простого нагружения, при котором внешние силы направлены вдоль продольной оси бруса, а их точки приложения совпадают с центром массы сечений.

Внутренние усилия.

В поперечных сечениях бруса возникает только нормаль-ная (продольная) сила N, которая в произвольном поперечном сечении численно равна алгебраической сумме проекций на его продольную ось х всех внешних сил, приложенных по одну сторону от рассматриваемого сечения (10.1).

Между интенсивностью внешней продольной силы q и внутренней нормальной силой N имеется соотношение

dN(x)/dx = q(x). (18)

Из геометрического смысла производной (первая производная равна тангенсу угла между касательной к кривой и осью абсцисс) следуют правила для проверки соответствия эпюры нормальной силы расчетной схеме:

1. Если на участке отсутствует распределенная нагрузка (q =0), то нормальная сила постоянна.

2. Если на участке имеется равномерно распределенная нагрузка, то нормальная сила изменяется по линейному закону.

3. В сечении, где приложена внешняя сосредоточенная сила, эпюра N имеет скачок на величину этой силы.

4. Эпюра должна выходить из нуля и уходить в нуль (вне твердого тела внутренней силы нет).

Напряжения.

Нормальные напряжения s в поперечном сечении бруса, как интенсивность действия нормальной силы по сечению, в соответствии с гипотезой плоских сечений распределены равномерно (рис.4) и поэтому

, (19)

где i – номер участка с соответствующей нормальной силой N и площадью сечения А.

Условие прочности

(20)

где [ ] или , зависящие от материала, берутся по справочникам.

 

Рис. 4. Эпюра нормальных напряжений в поперечном сечении и напряжения в наклонных сечениях при центральном растяжении

Перемещения.

Расчет абсолютного удлинения (укорочения) бруса ведется по закону Гука по участкам:

(21)

где Е – модуль продольной упругости (модуль упругости 1 рода или модуль Юнга), e - относительное удлинение.

Если изменяется вдоль оси бруса площадь сечения или внутренние усилия, то

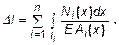(22)

Закон Гука верен только при упругих деформациях, когда напряжения не превышают предела пропорциональности.

При расчетах на растяжение нормальная сила, нормальное напряжение и перемещение (удлинение) положительны. Здесь знак имеет физический смысл, так как за пределом текучести σ _т поведение пластичных материалов и конструкций из них при растяжении и сжатии различается, а для хрупких материалов пределы прочности σ _в и соответственно допускаемые напряжения [ σ ] при растяжении меньше, чем при сжатии.

 

Пример 1.

Для заданной расчетной схемы (рис5,а) ступенчатого бруса оценить прочность конструкции и определить абсолютное удлинение. Брус имеет по длине три участка.

1. Реакция опоры.

Определяется из суммы проекций сил на ось х (10,1):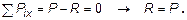

2. Внутренние усилия.

Эпюра внутренних усилий строится с применением метода сечений (рис. 2). Рассмотрим первый участок.

Задаваясь нормальной силой N, положительной по направлению, получим

.

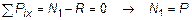Аналогично вычисляется нормальная сила и на других участках. В данном примере

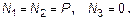
На рисунке 5,в приведена эпюра нормальных сил.

 

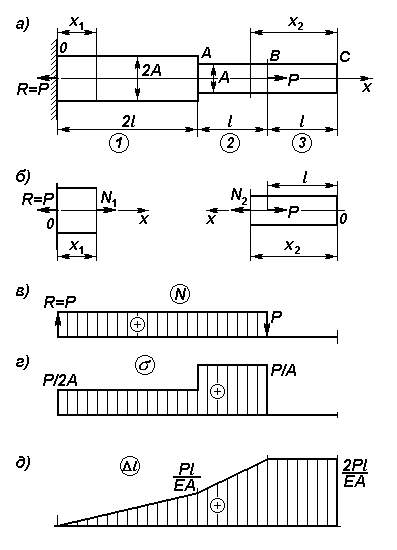
Рис. 5. Центральное растяжение–сжатие (к примеру 1):

а – расчетная схема; б – рассматриваемые отсеченные части;

в – эпюра нормальных сил; г – эпюра нормальных напряжений;

д – эпюра продольных перемещений

 

 

3. Напряжения.

Расчет нормальных напряжений в поперечном сечении бруса ведется по формуле (19). Для рассматриваемого примера получим:

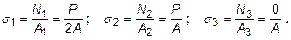
Эпюра нормальных напряжений приведена на рис. 5,г.

Для оценки прочности при проверочном расчете величина максимального напряжения сравнивается с допускаемым напряжением:

Величина перегрузки в расчете по допускаемым напряжениям не должна превышать 5%.

Условие прочности позволяет также определять допустимую грузоподъемность системы:

а также оптимальные размеры поперечного сечения (проектный расчет):

.

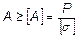4. Продольные перемещения.

Расчет удлинения бруса производится по закону Гука (21). Для рассматриваемого примера перемещение сечения А относительно 0 равно удлинению первого участка:

.

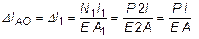Аналогично перемещение сечения В: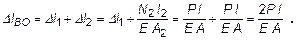

Полное удлинение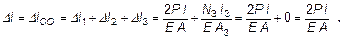

Эпюра перемещений приведена на рис. 5,д.

Характерно, что результат Δl _СВ = Δl ₃ = 0 не означает абсолютной неподвижности сечений на участке 3, они перемещаются относительно сечения 0 (сечения заделки).

Эпюры усилий, напряжений и перемещений могут быть определены или проверены достаточно оперативно, используя прием векторного замыкания эпюры N (рис. 5,в) и с использованием геометрического смысла (по площади) соотношения (19). А именно

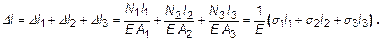Здесь σ _i× l _i – площади участков эпюры нормальных напряжений.

 

Вопросы для самопроверки

1. Какие тела называют упругими и упругопластичными? 2. В чем сущность метода сечений? 3. Что называют напряжением в данной точке сечения? 4. Какие напряжения называют нормальными? 5. Какие деформации являются упругими, а какие остаточными (пластическими)? 6. Как формулируется закон Гука? 7. Как определяют допустимые напряжения? 8. Что называют коэффициентом запаса прочности? 9. Каково условие прочности при растяжении? 10. Что называют пределом прочности и пределом текучести материала? 11. Что называют относительным остаточным удлинением при разрыве? 12. Что называют коэффициентом Пуассона и чему он равен? 13. Какие материалы называют хрупкими, а какие пластичными? 14. Как строится диаграмма растяжения?