Опасных сечений конструкций

Известно [6], что различают усилия внешние и внутренние. Внешние усилия (нагрузки) – это количественная мера механического взаимодействия двух различных тел. К ним относятся и реакции в связях. Внутренние усилия – это количественная мера механического взаимодействия двух частей одного тела, расположенных по разные стороны сечения, и вызванное действием внешних усилий. Внутренние усилия возникают непосредственно в деформируемом теле.

На рис.2,а приведена расчетная схема бруса с произвольной комбинацией внешних усилий, но образующих равновесную систему усилий:

. (1)

При этом реакции связей определяются из известных уравнений равновесия (статики) твердого тела [6]:

 

; ;

; ; (2)

; ,

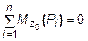где х₀ , у₀ , z₀ – базовая система координатных осей.

Мысленное разрезание бруса на две части произвольным сечением А (рис.2,а) требует выполнения условия равновесия для каждой из двух отсеченных частей (рис.2,б; 2,в). Здесь, как известно [1 – 4], { S′ } и { S" } – это внутренние усилия, возникающие соответственно в левой и правой отсеченных частях вследствие действия внешних усилий. Причем, при соединении мысленно отсеченных частей, условие равновесия тела обеспечивается соотношением

. (1а)

Так как исходная система внешних сил (1) эквивалентна нулю, получаем:

{ S ^′ } = – { S ^″ }. (3)

Это условие соответствует четвертой аксиоме статики о равенстве сил действия и противодействия. Используя общую методологию теоремыПуансо [6] о приведении произвольной системы сил к заданному центру и выбрав за полюс приведения сил центр масс сечения А' точку С' (рис.3,б), систему внутренних усилий для левой части { S' } сводим к главному вектору 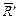и главному моменту внутренних усилий. Аналогичное приведение делается для правой отсеченной части, где положение центра масс сечения А″ определяется, соответственно, точкой С" (рис.2,в).

{ S′ } ~ { R′, L′ ₀ }; { S" } ~ { R", L" ₀ }. (4)

Здесь в соответствии с четвертой аксиомой статики по-прежнему имеют место следующие соотношения:

R′ = – R", L′ ₀ = – L" ₀. (5)

Таким образом, главный вектор и главный момент системы внутренних усилий, возникающие в левой условно отсеченной части бруса, равны по величине и противоположны по направлению главному вектору и главному моменту системы внутренних усилий, возникающим в правой условно отсеченной части.

 

Рис. 2. Метод сечений:

а – расчетная схема бруса, б – левая отсеченная часть, в – правая отсеченная часть

График (эпюра) распределения численных значений главного вектора и главного момента вдоль продольной оси бруса и предопределяют, прежде всего, конкретное решение задач обеспечения прочности, жесткости и надежности конструкций.

Определим способ нахождения компонент внутренних усилий, которые характеризуют простые виды сопротивлений: растяжение-сжатие, сдвиг, кручение и изгиб.

В центрах масс исследуемых сечений С' или С" зададимся соответственно левой (с', х', у', z') или правой (с", х", у", z ² ) СИСТЕМАМИ координатных осей (рис.2,б; 2,в), которые, в отличие от базовой системы координат x ₀ , у ₀ , z ₀ , будем называть “следящими”. Термин обусловлен их функциональным назначением. А именно: отслеживание изменения положения сечения А (рис.2,а) при условном смещении его вдоль продольной оси бруса, например при: 0 ≤ х ¢₁ ≤ а, а ≤ x ¢₂ ≤ b и т.д., где 0, а и b – линейные координаты границ исследуемых участков бруса.

Спроектируем главный вектор или и главный момент или на оси следящей системы координат (рис.2,б; 2,в):

{ N', Q' _y, Q' _z }; { M' _x, M' _y, M' _z }; (6)

{ N", Q" _y, Q" _z }; { M" _x, M" _y, M" _z }.

Эти проекции называются:

N – нормальная или продольная сила, возникает при центральном растяжении или сжатии;

М _x – внутренний крутящий момент, возникает при кручении;

Q _z, Q _у – поперечные или перерезывающие силы, возникают при сдвиговых деформациях;

М _у , М _z – внутренние изгибающие моменты, соответствуют изгибу.

При этом знак проекций главного вектора и главного момента внутренних усилий на оси следящей системы координат соответствуют правилам статики (в теоретической механике). Сила положительна, если ориентирована вдоль положительного направления оси. Момент положителен, если направлен против часовой стрелки, при наблюдении со стороны конца оси.

Общее число внутренних усилий в статически определимых задачах – шесть – совпадает с количеством уравнений равновесия для пространственной системы сил и связано с числом возможных взаимных перемещений одной условно отсеченной части тела по отношению к другой. Эти перемещения могут наблюдаться при разрушении тела по этому сечению.

Соединение левой и правой мысленно отсеченных частей бруса дает систему внешних и внутренних усилий, которая с учетом равновесия каждой отсеченной части имеет вид:

{ P ₁, P ₂, P ₃, …, N', N", Q ' _y, Q " _y, Q ' _z, Q" _z, M' _x, M" _x,

M' _y, M" _y, M' _z, M" _z, …, P _n-1, P _n } ~ 0. (7)

Анализ соотношения с учетом эквивалентности нулю исходной системы сил (1) дает:

{ N', N", Q' _y, Q" _y, Q' _z, Q" _z, М' _x, M" _x,

M' _y, M" _y, М' _z, M" _z }~ 0 (8)

Полученное условие, как естественное следствие из соотношений (3), (4), (5), приводит к необходимости образования одноименными компонентами внутренних усилий попарно подсистем эквивалентных нулю. То есть приходим к известному принципу равенства по модулю и противоположной направленности всех одноименных компонент внутренних усилий.

 

1){ N', N" } ~ 0 → N' = – N";

2) { Q' _y, Q" _y } ~ 0 → Q' _y = – Q" _y;

3) { Q' _z, Q" _z } ~ 0 → Q' _z = – Q" _{z .}; (9)

4) { М' _x, M" _x } ~ 0 → М' _x = – M" _x;

5) { M' _y, M" _y } ~ 0 → M' _y = – M" _y;

6) { М' _z, M" _z } ~ 0 → М' _z = – M" _z.

Искомые усилия определяют из соответствующих уравнений равновесия для любой из отсеченных частей, которые в следящей системе координатных осей приобретают вид:

1) _ix = N + P _1x + P _2x + … + P _kx = 0 → N;

2) _iy = Q _y + P _1y + P _2y + … + P _ky = 0 → Q _y;

3) _iz = Q _z + P _1z + P _2z + … + P _kz = 0 → Q _z;(10)

4) _x (P _i) = M _x + M _x (P _i) + … + M _x (P _k) = 0 → M _x;

5) _y (P _i) = M _y + M _y (P _i) + … + M _y (P _k) = 0 → M _y;

6) _z (P _i) = M _z + M _z (P _i) + … + M _z (P _k) = 0 → M _z.

Здесь для простоты обозначений системы координат с' х' у' z' и с" х" у" z" заменены единой c x у z.

Таким образом, метод построения эпюр внутренних усилий (в редакции освобождающей от механического запоминания правил знаков для внутренних усилий) включает этапы:

1. Определить реакции в связях по величине и направлению в базовой системе координат.

2. Определить количество участков бруса для использования метода сечений.

3. Мысленно разрезать брус в пределах исследуемого участка.

4. Изобразить по желанию левую или правую условно отсеченную часть.

5. Указать пределы изменения положения сечения (центра масс) вдоль продольной оси в базовой системе координат на этом участке.

6. Ввести в рассматриваемом сечении соответственно левую или правую следящую систему координатных осей.

7. Указать внутренние усилия (заменяющие действие условно отброшенной части бруса на рассматриваемую часть), взяв их положительными по направлению (в следящей системе координат).

8. Составить уравнения равновесия для рассматриваемой условно отсеченной части бруса в следящей системе координат.

9. Выразить из уравнений равновесия искомые внутренние усилия.

10. Вычислить значения искомых внутренних усилий на границах участков и, при необходимости, – их экстремальные значения.

11. Выбрав масштаб усилий, выполнить построение эпюры в соответствие с полученными их абсолютными значениями и знаками.

Указанная последовательность действий (кроме п.1) составляет суть метода сечений (разреза), единственного для определения внутренних усилий. В нем этапы 3,4,7 и 8 являются ключевыми. Естественно, что все способы контроля достоверности нахождения искомых внутренних усилий сохраняются: по замкнутости векторных многоугольников сил и моментов как свидетельства равновесия, свойств функций и их производных при исследовании изгиба и т.д. [1,3,4].

При наличии распределенной нагрузки в соответствие с теоремой Вариньона [6] векторный момент равнодействующей распределенной системы сил относительно любой точки равен сумме векторных моментов всех составляющих сил этой системы относительно той же точки.

Эпюра внутренних усилий позволяет достаточно просто, визуально найти положение опасного сечения, где действуют наибольшие по модулю внутренние усилия. В этом сечении наиболее вероятно разрушение конструкции при предельных нагрузках.