2017-11-01
2342
Лабораторная работа № 2
ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ
Цель: Изучение законов сохранения энергии и импульса.
Задача: определить скорости пули с помощью крутильного баллистического маятника ФПМ-09.
Оборудование: крутильный баллистический маятник ФПМ-09
Краткая теория
Прямолинейное движение.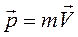 
- численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) материальной точки.
Закон сохранения импульса 
= const - импульс замкнутой системы не изменяется с течением времени.
Движение по окружности.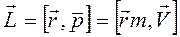 
- физическая величина, определяемая данным векторным произведением, называется моментом импульса (количества движения) материальной точки А относительно неподвижной оси О (см. рис.1), где 
-- радиус вектор, проведенный из точки О в точку A; 
=m 
- импульс материальной точки; 
- псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к 
.
|
|
|
 |
Модуль вектора момента импульса:
L = p r sinα = mV r sinα = pl,
где α - угол между векторами и ;. l - плечо вектора относительно точки О.
Закон сохранения момента импульса: = const. Момент импульса замкнутой системы относительно ее центра масс не изменяется с течением времени.
Закон сохранения энергии. В системе тел, между которыми действуют только консервативные силы, полная механическая энергия системы с течением времени остается постоянной
Е = Т + Р = const,
где Е - полная механическая энергия, Т - кинетическая энергия, Р -потенциальная энергия.
Кинетическая энергия механической системы - это энергия механического движения системы. Кинетическая энергия для
поступательного движения: 
, вращательного движения 
где J - момент инерции, ω - циклическая частота).
Потенциальная энергия системы тел - это энергия взаимодействия между телами системы (она зависит от взаимного расположения тел ивида взаимодействия между телами). Потенциальная энергия
упругодеформированного тела: 
; при деформации кручения 
где k – коэффициент жесткости (модуль кручения), х - деформация, α - угол кручения.
Абсолютно упругий удар - столкновение двух или нескольких тел, в результате которого во взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара вновь превращается в кинетическую энергию.
Абсолютно неупругий удар - столкновение двух или нескольких тел, в результате которого тела объединяются, двигаясь дальше как единое целое, часть кинетической энергии преобразуется во внутреннюю энергию.
|
|
|
Крутильный маятник - это система, совершающая крутильные (поворотные) колебания, см. рис.2.
Крутильные колебания возбуждаются за счет действия упругих сил, возникающих при деформации кручения проволоки (нити), к которой прикреплено колеблющееся тело. Период колебаний T при малых углах отклонения крутильного маятника определяется моментом инерции и модулем кручения проволоки по формуле
, где J - момент инерции;
k – модуль кручения проволоки.
Т еорема Гюйгенса-Штейнера: Момент инерции тела относительно любой оси АВ вращения J равен сумме момента его инерции Jo относительно параллельной оси 00, проходящей через центр масс тела и произведению массы тела на квадрат расстояния d между осями 00 и АВ (см. рис. 3).
J = J0+ md2
Вывод рабочей формулы
При выполнении работы необходимо, чтобы пуля при ударе залипала в мишени. Будем считать такой удар абсолютно неупругим и также будем считать, что силы трения в маятнике равны нулю.
На основании закона сохранения момента импульса для неупругого удара запишем:
mV l = (J1 + ml2)ω, (1)
где mV - момент импульса пули до удара (m — масса пули, V - скорость пули),
J1 + ml2 – момент инерции системы маятник-пуля (J1 - момент инерции собственно маятника, l - расстояние от оси вращения маятника до центра удара пули, ml2- момент инерции пули относительно оси маятника), ω - угловая скорость маятника.
На основании закона сохранения энергии для вращательного движения имеем:
½ (J1 + m l2)ω2= ½ kα2 (2)
k -модуль кручения проволоки, α - максимальный угол поворота маятника.
Используя (1) и (2) выразим скорость пули: левую и правую часть формулы (1) возьмем в квадрат
(m V l)2 = (J1 + ml2)2 ω2 → 
подставим данное выражение в формулу (2):
→ 
Так как момент инерции пули намного меньше момента инерции маятника ml2 «J1,
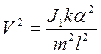(3)
Исключим из формулы (3) модуль кручения k и выразим момент инерции маятника J1 через величины, которые можно измерить.Период колебаний при малых углах отклонения крутильного маятника
Меняя положение грузов на стержне маятника, изменим момент инерции маятника и запишем:
- для первого положения грузов на стержне маятника момент инерции – J1
период колебаний 
- для второго положения грузов на стержне маятника момент инерции - J2
период колебаний. 
Тогда имеем 
; J1 − J2 = Δ J → J2 = J1 − Δ J; 
;
Выразим k из формулы периода для первого положения грузов 
;
Подставим два последних выражения в формулу (3):
.
Определим величину Δ J на основании теоремы Штейнера:
J1 = J0 + 2MR12; J2 = J0 + 2MR22,
Где J0 - момент инерции маятника, когда центр тяжестей грузов совпадает с осью вращения маятника; J1, J2 - момент инерции маятника при положении грузов на расстоянии R1, R2 от оси вращения.
Разность между моментами инерции Δ J = 2M(R12 - R22), тогда окончательное уравнение для скорости
T = t/n; t − показания миллисекундомера, n - число колебаний.
(рабочая формула),
где α - максимальный угол поворота маятника в момент удара для первого положения грузов на стержне маятника в радианной мере (по круговой шкале этот угол отмеряют в градусной мере φ= к, к – число делений по шкале, тогда α= (π/ 180)* φ
М - масса одного груза (173 г); m - масса пули; l - расстояние от оси вращения до центра удара пули; R1, R2 - расстояние от центров масс грузов до оси вращения маятника при первом и втором положении грузов на стержне, Т1 и Т2 - периоды колебаний маятника при первом и втором положении грузов на стержне, определяются по показаниям миллисекундомера T= t/n.
