Даны числа:  ,
,  . Тогда:
. Тогда:
1. 
2. 
3. 

Пример 1.
Даны числа: 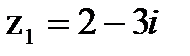 и
и 
Найти: а)  б)
б) 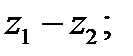
 в)
в)  г)
г) 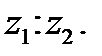
Решение. а) 
б) 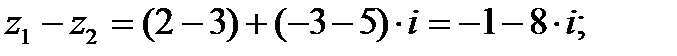
в) 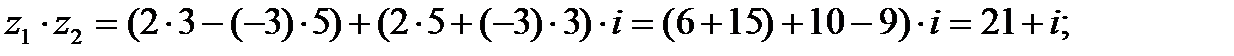 г)
г) 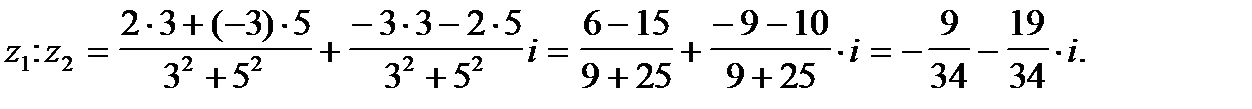
Пример 2. Решить уравнение 
Решение: т.к. aх2 + bx + c = 0, то 


Ответ: 

- 4 -
Упражнения.
№1.1. Дано: 

Найти: а)  б)
б) 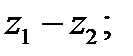 в)
в)  г)
г) 
№1.2. Решить уравнения:
а) 
| б) 
| в) 
|
Ответы. № 1.1. а) 5 – i; б) 1–11 i; б) 36 + 3 i; г) –24/29 – (27/29) i;
д) –48 – 16 i. №1.2. а) 2 +  i; 2 –
i; 2 –  i; б) 5/2 + (
i; б) 5/2 + ( /2) i;
/2) i;
5/2 – ( /2) i;в) – 1 + 2 i; – 1 – 2 i.
/2) i;в) – 1 + 2 i; – 1 – 2 i.
Тема 1.2. Основные понятия и методы дифференциального и интегрального исчисления. Предел функции.
Студент должен:
Знать: понятие предела функции; виды интегралов, таблицу основных интегралов; формулы для вычисления объема фигур;
Уметь: вычислять простейшие пределы; вычислять простые интегралы, применять при вычислении объемов тел вращения.
Предел функции.
Определение. Число b называется пределом функции f(x) в точке а при х, стремящемся к а. Это записывается так: 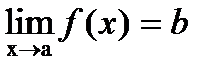 .
.
Теоремы о пределах:
 (С - число);
(С - число); 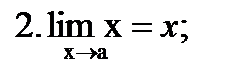



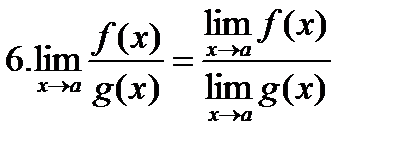 . Примеры. Вычислить пределы:
. Примеры. Вычислить пределы:



 т.к. х - 2 = 0, то разложим числитель дроби на
т.к. х - 2 = 0, то разложим числитель дроби на
- 5 -
множители: 

 Значит
Значит 
Тогда 
5. 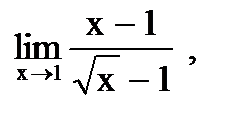 т.к. при х = 1 числитель и знаменатель дроби
т.к. при х = 1 числитель и знаменатель дроби
равны нулю, то домножим их на  получим:
получим: 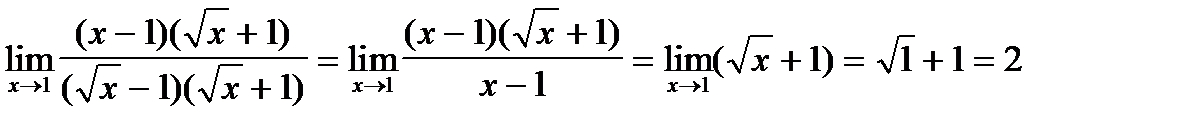 .
.
Упражнения. №2.1. Вычислить пределы.
а)  б)
б)  в)
в)  ; ;
| г) 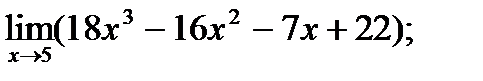 д)
д)  е)
е) 
|
| Ответы. №2.1. а) 369; б) 2; в) 27; | г) 1837; д) 0; е) – 0,125. |
Интеграл и его виды.
Определение 1. Совокупность всех первообразных функции  называется неопределенным интегралом и обозначается
называется неопределенным интегралом и обозначается  Вычисляется неопределенный интеграл по формуле:
Вычисляется неопределенный интеграл по формуле: 
 - знак интеграла, f(x) - подынтегральная
- знак интеграла, f(x) - подынтегральная
функция, 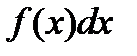 - подынтегральное выражение, F(x)- первообразная для функции f(x), С - постоянная.
- подынтегральное выражение, F(x)- первообразная для функции f(x), С - постоянная.
Определение 2. Под определенным интегралом 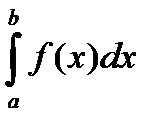 от данной непрерывной функции f(x) на отрезке
от данной непрерывной функции f(x) на отрезке  понимается соответствующее приращение ее первообразной, то есть
понимается соответствующее приращение ее первообразной, то есть
- 6 -
 (формула Ньютона-Лейбница), где а и в - границы интегрирования, F(b) и F(a) - значения первообразной в границах интегрирования.
(формула Ньютона-Лейбница), где а и в - границы интегрирования, F(b) и F(a) - значения первообразной в границах интегрирования.
Таблица интегралов:
1. 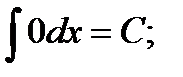 2.
2. 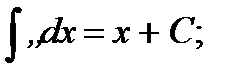 3.
3.  4.
4.  5.
5. 
| 6. 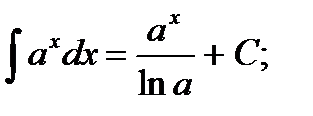 7.
7.  8.
8.  9.
9. 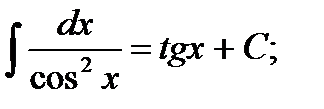 10.
10. 
|
Примеры. Вычислить интегралы:
а) 
б) 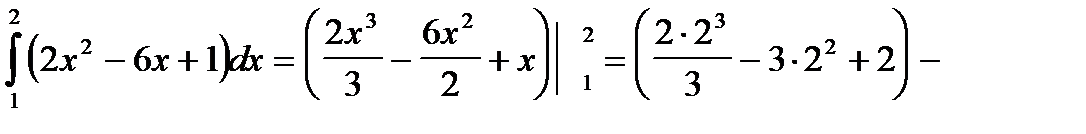

 2017-11-01
2017-11-01 337
337








