Матрицы и действия над ними

Матрицы как, системы линейных уравнений и определители применяются при решении экономических и технических задач.

Таблица вида называется матрицей размера где m - число строк, n - число столбцов.

Если матрица размера то ее называют квадратной порядка n, если то прямоугольной, размера .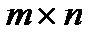

Произведением числа на матрицу называется матрица, где каждый элемент умножен на заданное число.

Например, то

Сумма и разность двух матриц одинакового размера получается сложением или вычитанием элементов, стоящих на одинаковых местах.

Например,

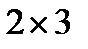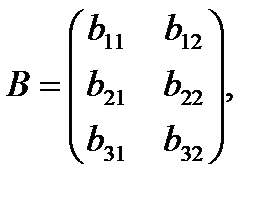Произведение матриц. а) Если даны матрицы и : то

- 15 -

б) Если даны квадратные матрицы размеров :

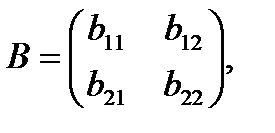то

То есть каждый элемент матрицы определяется по формуле:

где i - номер строки,

k - номер столбца. Значит, 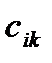представляет собой сумму парных произведений элементов i-ой строки первого сомножителя на соответствующие им по порядку следования элементы k-ого столбца второго сомножителя. Произведение выполняется только для матриц размеров и или и

Например. 1)

Например. 2)

Упражнения.

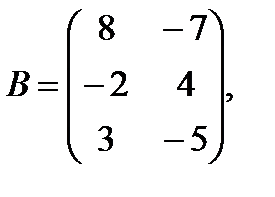
№7.1. Дано: . Найти:

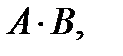
№7.2. Дано: , .

- 16 -

Найти:

№7.3. Фирма выпускает три вида продукции, используя два типа сырья. Затраченные ресурсы записаны в матрице А. План выпуска продукции в матрице С, а стоимость единицы каждого типа сырья в матрице В. Найдите общую стоимость сырья по формуле:

Q = C ^. (A ^.B), если А = , В = , С = .