Тема 3.1.1. Основные понятия и методы аналитической

Геометрии и векторной алгебре

Студент должен:

Знать: формулы для составления уравнений прямой, проходящей через две точки в плоскости;

Уметь: применять данные формулы при решении упражнений.

Уравнение прямой на плоскости, проходящей через две точки

Пусть даны точки: А(х₁, у₁), В(х₂, у₂).

Тогда уравнение прямой АВ представляется формулами:

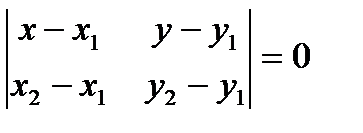или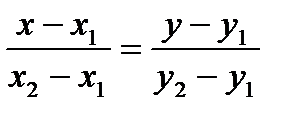

Преобразовывая эти формулы, получим уравнение прямой 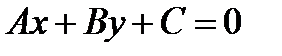(общий вид уравнения).

Пример. Составить уравнение прямой, проходящей через точки А(1;5), В(3;9).

Решение. Составим определитель и преобразуем его:

, ,

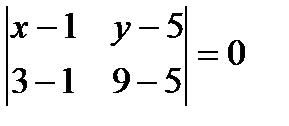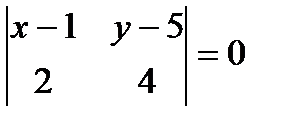- 17 -

,

,

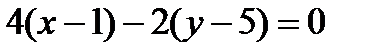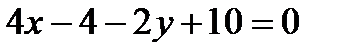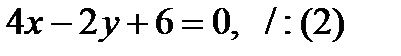
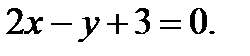
Ответ: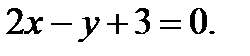

Уравнение плоскости, проходящей через три точки

Даны точки А(x₁;y₁;z₁), B(x₂;y₂;z₂), C(x₃;y₃;z₃), тогда уравнение плоскости, проходящей через точки А, В, С составляется по

формуле: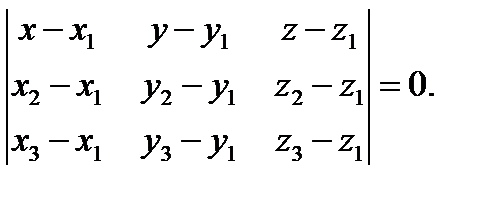

Преобразуя данную формулу, получим уравнение плоскости: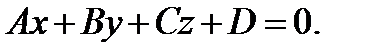

Пример. Составить уравнение плоскости, проходящей через точки. А(-1;4;-1), В(-13;2;-10), С(6;0;12).

Решение. Применяя формулу, получим: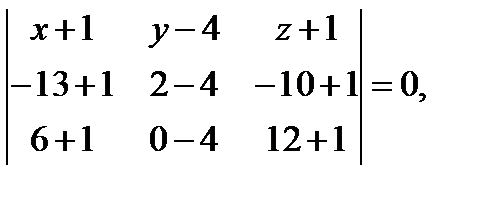

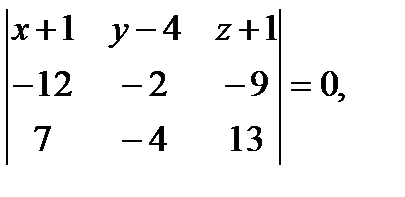
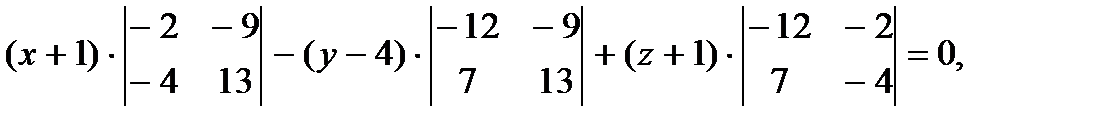
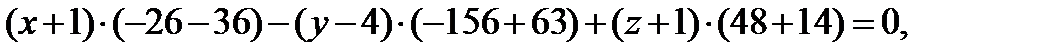
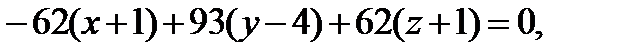
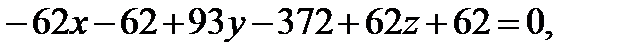
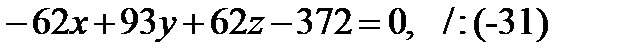
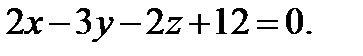
Ответ: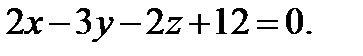

 

- 22 -

Упражнения.

№ 8.1. Составить уравнение прямой, проходящей через точки:

а) А(1;4), В(2; – 3). [7х + у – 11 = 0]

б) C(–5;3), D(9;4). [х – 14у + 47 = 0]

в) K(– 6;1), P(2; – 1). [х + 4у + 2 = 0.]

№8.3. Составить уравнение плоскости, проходящей через три точки:

а) А(2;0;2), В(4;1;2), C(2;0;4). [ х – 2у – 2 = 0 ]

б) А(–1;5;3), В(2;3; –1), C(4;0; –1). [ 12х + 8у + 5z – 43 = 0 ]