Рискового инвестора

Лекция 6. ОПТИМАЛЬНЫЙ ПОРТФЕЛЬ

Рассмотрим решение задачи составления оптимального портфеля для рискового инвестора. Для этого запишем задачу (30)-(32) в виде задачи нелинейного программирования:

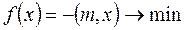
при условиях

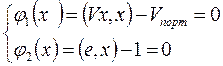
Теорема о множителях Лагранжа может быть применена, если градиенты ограничений.

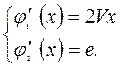
линейно независимы.

Если существует 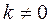, что

,

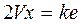то вектора зависимы, тогда

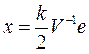
Может ли этот вектор быть решением задачи нужно исследовать отдельно.

Предположим, что такого k не существует, тогда градиенты линейно независимы и применима теорема о необходимом условии. Из теоремы следует, что существуют два числа 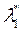,,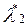 такие, что для решения x^* справедливо равенство:

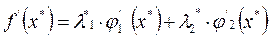
или

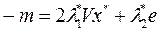
Решим уравнение относительно :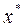

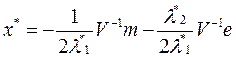
Найдем 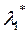и 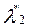. Для этого подставим (50) в (44) и (45). Получим два уравнения для двух неизвестных:

,

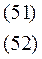
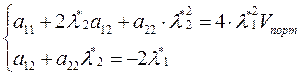где коэффициенты a₁₁, a₁₂, a₂₂ вычисляются как и в предыдущей главе.

Алгоритм расчета.

1. Из уравнения (52) выражаем 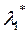и подставляем в уравнение (51). Получаем квадратное уравнение относительно 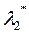. Получаем в общем случае два решения: 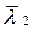и .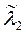

2. Из уравнения (52) находим 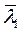и 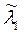(соответственно).

3. Подставляем соответствующие множители Лагранжа в (50) и находим из (50)два вектора: 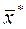и .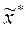

4. Определяем, какой из этих векторов является решением задачи.

5. Находим эффективность портфеля ценных бумаг.

6. Проводим анализ решения.