Оптимальный комбинированный портфель рассчитывается в случае, когда за счет одновременной покупки безрисковой и рисковых ценных бумаг хотят добиться новых инвестиционных качеств портфеля.
8.1. Запишем задачу составления комбинированного портфеля в виде стандартной задачи нелинейного программирования.
Предположим, что решено купить один вид безрисковой ценной бумаги с эффективностью r %- годовых, и n -видов ценных бумаг Ri с характеристиками, mi, si, Vij. Обозначим долю капитала, идущую на покупку безрисковой ценной бумаги x0, и соответственно, x1, x2,…,xn - доли, идущие на покупку рисковых ценных бумаг. Тогда вектор распределения всех долей имеет вид:
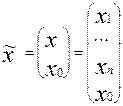
При расчете риска комбинированного портфеля учитываем лишь риски рисковых ценных бумаг и получаем для осторожного инвестора целевую функцию:
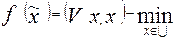
Где множество U определяется следующими ограничениями:
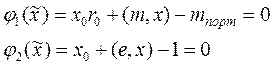
Причем к этим ограничением могут добавляться еще ограничения 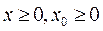 , но в этом случае задача не допускает точного решения, и поэтому в данной главе ограничения не отрицательности не учитываются.
, но в этом случае задача не допускает точного решения, и поэтому в данной главе ограничения не отрицательности не учитываются.
В постановке задачи из экономических соображений следует mпорт>r0, причем величина mпорт - r0 – называется премией за риск.
8.2. Решение. Рассчитаем 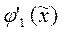 ,
, 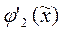 и
и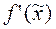 :
:
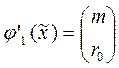 ,
, 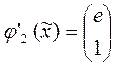 ,
, 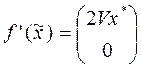
Вектора 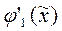 и
и 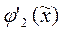 - линейно-независимы, так как обычно существует такое то
- линейно-независимы, так как обычно существует такое то 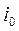 , что
, что 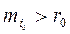 .
.
Применяя правило множителей Лагранжа, получаем:
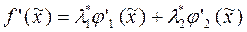
или иначе
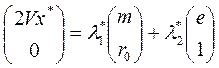
Используя, эти уравнения и уравнения ограничений получаем систему уравнений:
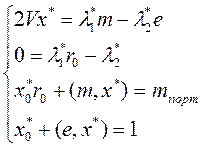
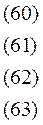
Из второго уравнения системы получаем равенство
(64)
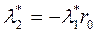 ,
,
которое подставляем в первое уравнение
|
 2014-01-28
2014-01-28 729
729








