2.
1.
Таблица№1.
Задача.
Итак
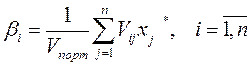
Запишем эту формулу в векторной форме:
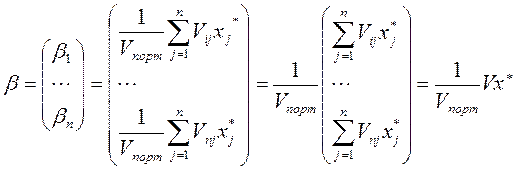 ,
,
где V - матрица ковариации.
Так как
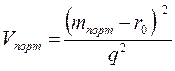
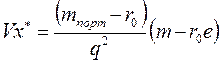 ,
,
то для 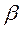 получим формулу:
получим формулу:
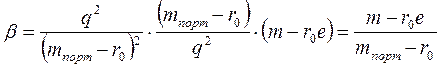
или
|
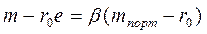 ,
,
здесь 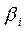 - доля общей информации за риск, приходящийся на данную ценную бумагу.
- доля общей информации за риск, приходящийся на данную ценную бумагу.
Теорема доказана.
Вывод:
С учетом доказанных теорем получаем, что бета вклада является весьма полной характеристикой вклада данной ценной бумаги в портфель.
На рынке имеется одна безрисковая ценная бумага с эффективностью 2% годовых и три независимых рисковых ценных бумаги, характеристики которых приведены в таблице№1.
| Характеристики | |||
| mi | 8% | 10% | 15% |
| si | 7% | 10% | 60% |
Найдем такое распределение капитала по всем четырем ценным бумагам, чтобы риск был минимальным. Рассмотрим два различных случая:
1. когда инвестор желает, чтобы mпорт = 9%;
2. когда инвестор желает, чтобы mпорт = 11%.
Сравним результаты и проведем их анализ.
Решение:
1) В данном случае r0 = 2%, mпор т = 9%.
2) 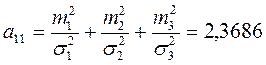
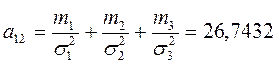
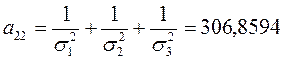
3) 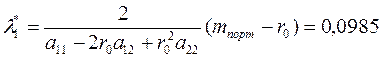
4) 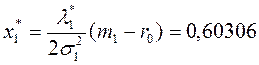
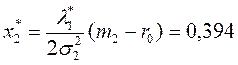
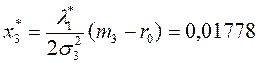
5) 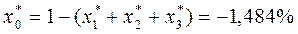
6) 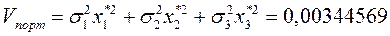
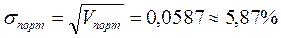
1) В данном случае r0 = 2%, mпорт = 11%.
2) Числа а11, а12, а22 уже рассчитаны выше.
3) 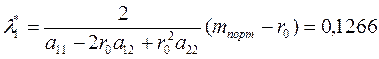
4) 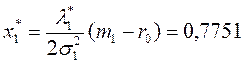
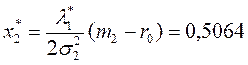
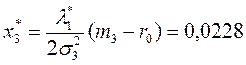
5) 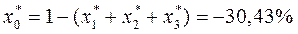
6) 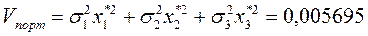
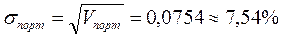
1случай:
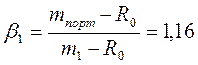
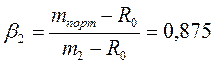
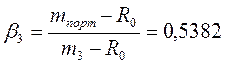
2случай:
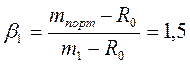
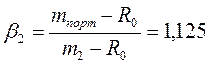
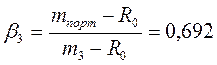
 2014-01-28
2014-01-28 669
669








