Инвестиции: определение и классификация. Разделение решений об инвестициях и о потреблении. Инвестиции в основной какитал: неоклассический подход. Модель простого акселератора. Модель гибкого акселератора. Теория инвестиций q-Тобина.
Инвестиции являются одним из основных факторов, определяющих рост экономики в долгосрочной перспективе.
Инвестиции: определение и классификация
Вспомним, что же мы понимаем под инвестициями в макроэкономике? Инвестиции - это расходы, направляемые на увеличение и сохранение основного капитала. Основной капитал состоит из зданий, оборудования, сооружений и др. элементов с длительным сроком службы, используемых в процессе производства. Следует отметить, что к инвестициям не относят следующие операции: покупку уже существующих инвестиционных благ, приобретение акций, облигаций и других ценных бумаг.
Различают валовые и чистые инвестиции. Валовые инвестиции представляют собой совокупность всех инвестиционных расходов, в то время как чистые инвестиции равны чистому приросту основного капитала. Таким образом, в чистые инвестиции не включают амортизационные расходы, то есть расходы, связанные с возмещением физически изношенного или морально устаревшего капитала. Считая, что амортизация пропорциональна имеющемуся на данный момент запасу капитала и, обозначив норму амортизации через d, получим следующее соотношение между чистыми It и валовыми Itg инвестициями периода t:
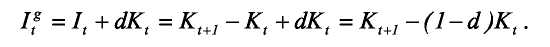
Все инвестиционные расходы подразделяются на 3 категории:
1) инвестиции в основной капитал (расходы на покупку машин, оборудования, строительство заводов, фабрик, офисов)
2) инвестиции в жилищное строительство (строительство и текущие расходы по поддержанию жилого фонда)
3) инвестиции в товарно-материальные запасы
Мы сконцентрируем наше внимание лишь на первой категории.
Рассматривая современные теории потребления, мы пришли к выводу, что потребители предпочитают сглаженное потребление, но в отношении инвестиций дело обстоит иначе. Инвестиционные расходы обладают большой изменчивостью. Еще Кейнс отметил, что именно изменения в уровне инвестиций являются движущей силой цикла деловой активности.
Следует отметить, что подсчет инвестиционных расходов, используемый в системе национальных счетов не совсем корректен. Так, например, расходы домохозяйств на товары длительного пользования (машины, холодильники и т.п.) включают в потребление, несмотря на то, что эти товары, будучи однажды приобретенными, создают услуги в течение ряда последующих лет и, следовательно, их следовало бы отнести к инвестиционным расходам. Кроме того, в системе национальных счетов под инвестициями понимается лишь изменение физического капитала, в то время как изменение человеческого капитала в результате роста уровня образования и накопления знаний на сегодняшний день в инвестиционных расходах не учитывается. Например, расходы на образование, как и расходы на приобретение товаров длительного пользования, в системе национальных счетов принято относить к потреблению. В результате уровень инвестиционных расходов сильно недооценивается.
Разделение решения об инвестициях и решения о потреблении (теорема отделимости)
Рассмотрим двухпериодную модель для домохозяйства, как мы это делали при выборе решения о потреблении, однако введем дополнительные возможности для перераспределения ресурсов между периодами. Предположим, что часть ресурсов (I1) в первом периоде можно направить на инвестиции, которые позволят увеличить выпуск во втором периоде на величину F(K), где F(K) - производственная функция и K=K0+I1. Считая, что капитал полностью изнашивается за один период, получаем следующее бюджетное ограничение:
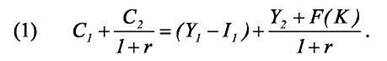
Задача потребителя заключается в оптимальном выборе потребления в каждом периоде и объема инвестиций, то есть потребитель максимизирует функцию полезности при ограничении (1)
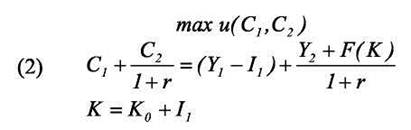
Будем считать, что первоначальный запас капитала равен нулю (K0 =0) и изобразим решение задачи (2) графически (смотри рис.1).
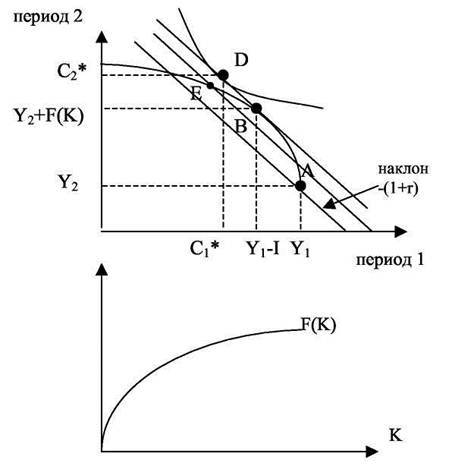
Рис. 1. Разделение решений о производстве и потреблении в двухпериодной модели.
Первоначальный запас потребителя представлен на рисунке точкой A. Если бы не было возможностей для инвестирования, то потребитель выбирал бы оптимальное потребление на бюджетной линии, проходящей через точку А с наклоном, равным - (1+r), где r -реальная ставка процента. Возможность инвестирования позволяет потребителю расширить бюджетное множество. Эти возможности отражены на рисунке с помощью производственной функции F(K), которая наложена на рисунок в зеркальном отражении с началом координат в точке А. Таким образом, путем инвестирования потребитель может изменить доставшийся ему первоначальный запас, сдвинувшись вдоль кривой, отражающей производственные возможности, в любую точку левее точки А, например, в точку Е. В силу того, что ставка процента по кредитам совпадает со ставкой процента по депозитам, наклон бюджетного ограничения будет одинаков слева и справа от точки производства Соответственно в этом случае бюджетное ограничение потребителя будет представлено прямой с наклоном -(1+r), проходящей через выбранную точку (например, Е).
Как видно из рисунка 1, решение о производстве непосредственно отразится на бюджетном множестве потребителя: изменяя наше решение об инвестициях мы можем расширить бюджетное множество. Так, перейдя из исходной точки А в Е мы добились сдвига бюджетного ограничения вправо-ввверх, что увеличило количество доступных потребителю наборов. Однако данный уровень инвестиций не является наилучшим, поскольку мы могли бы немного уменьшив инвестиции, перейти в точку В, что позволило бы нам включить в бюджетное множество целую область ранее не доступных потребителю наборов. Заметим, что сдвинувшись из точки В влево или вправо мы лишь потеряем ряд потребительских наборов, но ничего не приобретем взамен, таким образом точка В дает максимально большое бюджетное множество. Таким образом, выбрав уровень инвестиций, соответствующий точке В, мы получим все возможные потребительские наборы, которые были бы доступны потребителю при любых других инвестиционных решениях. Это означает, что в данном множестве заведомо содержится оптимальный набор, каковы бы ни были предпочтения данного потребителя. Итак, как мы показали, решение о производстве не зависит от вида кривых безразличия, поскольку главная задача при выборе уровня инвестиционных расходов заключается в том, чтобы максимально расширить бюджетное множество потребителя. Для этого индивидууму следует выбрать максимальный уровень богатства (W), которое в данном случае может быть представлено следующим
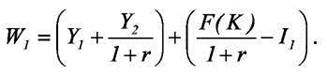
Для максимизации богатства необходимо найти такую точку на границе множества производственных возможностей, в которой наклон равен -(1+r). Действительно из условия первого порядка для задачи (2) имеем:
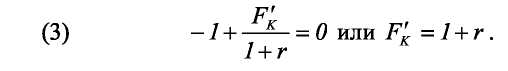
В результате получаем, что производить нужно в точке В, а оптимальное потребление будет в точке D.
Итак, задача домохозяйства разбивается на две самостоятельные задачи. На первом шаге осуществляется выбор оптимального уровня инвестиций путем решения задачи максимизации богатства, а на втором шаге решается стандартная задача выбора оптимального потребления при заданном уровне богатства. Заметим, что подобное разбиение возможно только при условии совершенства финансового рынка, то есть, требуется совпадение ставок процента по кредитам и депозитам.
Этот результат имеет важное значение, поскольку позволяет делегировать решение о выборе инвестиций другому агенту (например, менеджеру), поставив перед ним задачу максимизации богатства, при этом разница в предпочтениях этих агентов не оказывает влияния на оптимальность принимаемого решения. Полученный нами вывод о возможности разделения решения о потреблении и решения о производстве носит название теоремы отделимости.
Инвестиции в основной капитал: неоклассический подход
Теорема об отделимости позволяет нам рассматривать решение о производстве отдельно от решения о потреблении. Уточним, каким же критерием следует руководствоваться менеджерам при выборе оптимального уровня инвестиций. Как показывает теория решение должно приниматься, исходя из критерия максимизации богатства. Учитывая, что потребители могут владеть лишь долей в некоторой фирме или же владеть долями в нескольких фирмах, максимизации богатства каждого из владельцев эквивалентна максимизации рыночной стоимости каждой фирмы, которая равна приведенной стоимости потока дивидендов (напомним, что дивиденды платятся из прибыли фирмы).
Рассмотрим фирму, которая производит продукцию, используя два фактора производства труд (L) и капитал (K). Технология описывается производственной функцией F(K,L). Будем считать, что функция возрастает по каждому аргументу и строго вогнута по совокупности аргументов так, что в результате предельный продукт каждого фактора положителен и убывает с ростом данного фактора
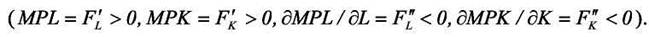
Пусть p - цена готовой продукции, pK - цена единицы инвестиционных благ, w - ставка заработной платы. Будем считать, что норма амортизации постоянна и равна d. Пусть инвестиционный лаг равняется одному периоду, то есть, инвестиции, осуществленные в период t, трансформируются в капитал и могут быть использованы в процессе производства в следующем периоде t+1. При этих условиях прибыль фирмы (до выплаты дивидендов) в период t - (φt) равна:
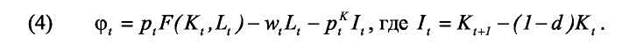
Менеджер выбирает оптимальный уровень инвестиций, решая задачу максимизации рыночной стоимости фирмы (V), равной приведенному потоку прибыли фирмы:
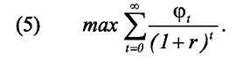
Выпишем условия первого порядка для этой задачи:
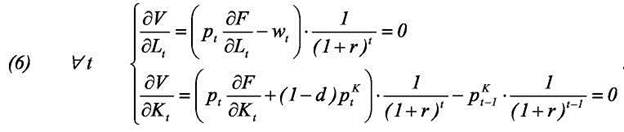
Из первого условия получаем, что предельный продукт труда должен быть равен реальной заработной плате:
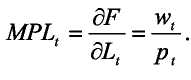
Нас больше интересует второе условие, поскольку оно связано с выбором оптимального уровня капитала. После преобразований получаем:
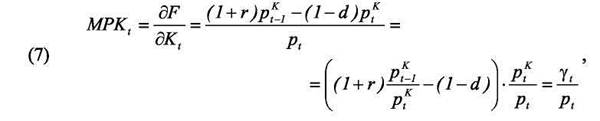
где γt - издержки на единицу капитала Йоргенсона. Преобразуем выражение для издержек капитала, обозначив через ρ темп удорожания единицы капитальных благ (то есть pt /pt-1K =1+ ρt), тогда
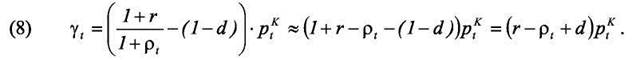
Таким образом,
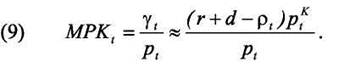
Итак, что же скрывается за издержками на единицу капитальных благ γt? Еще ранее при построении функции инвестиций мы отмечали, что ставка процента является ключевым параметров, влияющим на инвестиции. Теперь мы видим, что нужно принимать во внимание тот факт, что капитал изнашивается в процессе производства, а потому норма амортизации также влияет на издержки капитала. Кроме того, если мы рассматриваем многопродуктовую модель, то следует учитывать, что стоимость капитальных благ также может изменяться по отношению к стоимости выпускаемой продукции. Удорожание капитальных благ означает, что купленную ранее единицу капитального блага теперь мы можем продать дороже и, соответственно, издержки на единицу капитальных благ снижаются на величину выигрыша от удорожания.
Обсудим, почему условие, определяющее оптимальный уровень капитала (9) отличается от условия, полученного ранее для двух двухпериодной модели (MPK = FK′ = 1 + r)? Вспомним основные предпосылки этой модели. Во-первых, мы рассматривали однопродуктовую экономику, то есть цена капитала совпадала с ценой производимой продукции (ptK = pt), более того, мы считали, что инфляция отсутствует, и цены не меняются со временем, то есть ρ=0. Помимо этого, мы предполагали, что капитал полностью изнашивается за один период, то есть d=1. Нетрудно увидеть, что при этих предположениях выражение (9) в точности совпадает с полученным ранее условием (3).
Проанализируем условие (9). Будем считать, что капитал предыдущего периода и занятость в текущем периоде заданы (Kt-1 = , Lt = L), тогда увеличение капитала в период t означает увеличение инвестиций. Учитывая предположение об убывании предельного продукта капитала, мы можем представить оптимальный уровень капитала K* в период t графически (смотри рисунок 2). Для простоты будем считать, что имеем дело с однопродуктовой моделью так, что условие (9) принимает вид MPK=γ. Что произойдет с оптимальным уровнем капитала, если издержки капитала (γ) возрастут? Как видно из графика, рост издержек приведет к падению оптимального уровня капитала, то есть, к сокращению инвестиций. Повышение γ приводит к тому, что отдача от дополнительной единицы капитала (MPK) не покрывает издержек γ, что влечет сокращение запаса капитала. Итак, повышение реальной процентной ставки, увеличение нормы амортизации и снижение темпа роста цен капитальных благ ведут к росту γ, а значит, к сокращению капитала и падению чистых инвестиций.
, Lt = L), тогда увеличение капитала в период t означает увеличение инвестиций. Учитывая предположение об убывании предельного продукта капитала, мы можем представить оптимальный уровень капитала K* в период t графически (смотри рисунок 2). Для простоты будем считать, что имеем дело с однопродуктовой моделью так, что условие (9) принимает вид MPK=γ. Что произойдет с оптимальным уровнем капитала, если издержки капитала (γ) возрастут? Как видно из графика, рост издержек приведет к падению оптимального уровня капитала, то есть, к сокращению инвестиций. Повышение γ приводит к тому, что отдача от дополнительной единицы капитала (MPK) не покрывает издержек γ, что влечет сокращение запаса капитала. Итак, повышение реальной процентной ставки, увеличение нормы амортизации и снижение темпа роста цен капитальных благ ведут к росту γ, а значит, к сокращению капитала и падению чистых инвестиций.
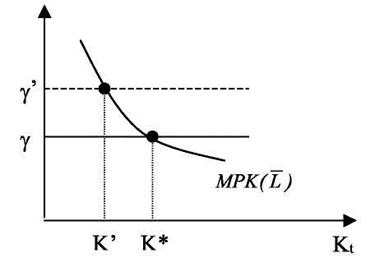
Рис. 2. Влияние издержек капитала на выбор оптимальной величины капитала.
Следует отметить еще один важный момент. Как мы видели, инвестиции отрицательно зависят от реальной ставки процента r. Однако в реальности никто не знает, каково же будет значение реальной процентной ставки, поскольку никто не может точно определить величину инфляции. Принимая решения, инвесторы ориентируются на ожидаемую реальную ставку процента (rexp), которая получается из номинальной процентной ставки (i) с поправкой на ожидаемую инфляцию (πexp):
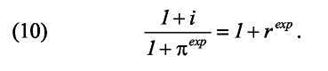
При небольшом уровне инфляции можно использовать приблизительное соотношение:
(11) rexp ≈ i−πexp.
Заметим, что предельный продукт капитала на рисунке 2 изображен при данном уровне занятости. Если занятость изменится, то сдвинется и кривая предельного продукта капитала, что отразится на оптимальной величине капитала и инвестициях. Будем считать, что труд и капитал являются факторами комплиментарными, то есть с увеличением одного из факторов предельный продукт другого фактора возрастает. Это означает, что рост занятости (вызванный, например, падением реальной заработной платы) приведет к сдвигу вверх кривой предельного продукта капитала, что вызовет рост оптимальной величины капитала и увеличение инвестиций.
Итак, поскольку в рассматриваемой модели инвестиции были равны изменению запаса капитала, то на основе полученные выводов о параметрах, влияющих на величину оптимального запаса капитала можно сделать следующие заключения относительно изменения инвестиций. Увеличение ожидаемой реальной процентной ставки, увеличение нормы амортизации и ожидаемое (в будущем) относительное удешевление капитальных благ влечет рост издержек капитала, что приводит к падению оптимальной величины капитала и, соответственно, (при заданном первоначальном запасе капитала) к снижению инвестиций. Ожидаемый рост занятости (в силу ожидаемого роста продаж), как мы видели, положительно влияет на оптимальный запас капитала и, соответственно, стимулирует инвестиции.
Эмпирические исследования инвестиционных расходов.
Рассмотренные выше теоретические модели позволили нам выделить ряд параметров, влияющих на динамику инвестиций. В частности, мы убедились в существовании отрицательной зависимости между инвестиционными расходами и ставкой процента. Однако этого недостаточно, чтобы объяснить некоторые особенности в поведении инвестиционных расходов. Теперь мы обратимся к простейшим эмпирическим моделям инвестиций, каждая из которых обладает рядом достоинства и недостатков.
 2014-01-28
2014-01-28 2269
2269
