Решение нелинейных уравнений в Excel

Нелинейные уравнения – это уравнения вида f(x)=0, где f(x) – нелинейная функция. Решение уравнения f(x)=0 сводится к поиску таких значений х^* (корней уравнения), которые превращают уравнение в тождество. Различают нелинейные алгебраические уравнения и трансцендентные.

Например, нелинейное алгебраическое уравнение ax² + вx +с =0 имеет два корня, которые могут быть действительными или мнимыми. Например, уравнение х² + 2=0 имеет два мнимых корня х₁= Ö-2 и х₂= -Ö-2.

В дальнейшем будет идти речь о вычислении только действительных корней.

Трансцендентным называется уравнение,если в f(x) входит хотя бы одна трансцендентная функция. Например, sin(x) –1=0;

Решение нелинейных уравнений выполняют в два этапа:

1. Этап отделения корней.

2. Этап уточнения корней, т.е. поиск коней с заданной точностью.

Этап отделения корней

Для этого построим график заданной функции f(x)=0. В столбце А располагаем изменение аргумента, а в столбце В табулируемую функцию. Строим график. На графике выделяем границы корня и в этих границах берем начальное приближение корня (нарисовать график, выделить корни и взять начальное приближение).

Этап уточнение корня

Команда Подбор параметров

Порядок уточнения:

1. В ячейку A1 вводим начальное приближение корня Х₁.

2. В ячейку В1 вводим формулу с заданной функцией.

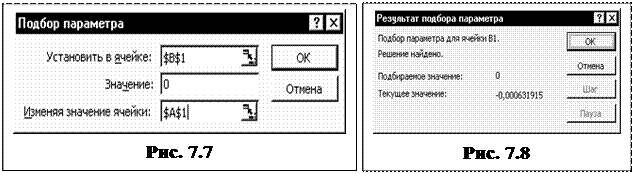
3. Выполняем команды Сервис, Подбор параметра. Появляется окно Подбор параметра (рис. 7.7).

4. В поле "Установить в ячейке" записать адрес первой формулы (можно снять окно и щелкнуть ячейку В1, затем восстановить окно).

5. В поле "Значение" установить 0.

6. В поле "Изменяя значение ячейки" установить адрес А1 (снять окно и щелкнуть А1).

7. Щелкнуть ОК. Появляется окно Результат подбора параметра (рис. 7.8), а в ячейке А1 будет уточненное значение корня.