§1. Постановка задачи. Основные определения. Рассмотрим нелинейное уравнение f(x)=0. Корнем этого уравнения называется значение 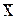 , при котором
, при котором 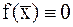 . Решение уравнения заключается в нахождение его корней. Корень
. Решение уравнения заключается в нахождение его корней. Корень 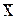 называется простым, если
называется простым, если 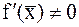 . Корень называется кратным, если
. Корень называется кратным, если 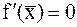 . Целое число m называется кратностью корня
. Целое число m называется кратностью корня 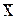 , если
, если 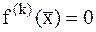 для k=1,2,3...(m-1), а
для k=1,2,3...(m-1), а 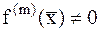 . Случай k=1 соответствует простому корню.
. Случай k=1 соответствует простому корню.
Рассмотрим график некоторой функции y=f(x) (xÎ[a,b]), который представлен на рис.1. Из определения следует, что корень является простым, если график функции y=f(x) пересекает ось 0x в точке 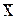 под yглом a¹0
под yглом a¹0 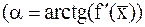 , и кратным, если он касается оси 0x в точке
, и кратным, если он касается оси 0x в точке 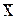 , т.к. имеем a=0.
, т.к. имеем a=0.
Существуют следующие методы решения нелинейных уравнений: аналитические, графические и численные. Аналитическими методами удается воспользоваться только для уравнений определенного вида, в общем случае они не применимы. Графические методы естественно обладают большой погрешностью. Поэтому основными методами являются численные методы.
Численное решение задачи нахождения корней нелинейного уравнения осуществляется в два этапа: этапа локализации корней и этапа итерационного уточнения корней.
На этапе локализации выделяется отрезок, содержащий только один корень, при этом длину этого отрезка стараются сделать как можно меньше. Поэтому предварительно проводится исследование уравнения, т.е. определяется существование корней уравнения, сколько их и как они расположены на числовой оси.
Для локализации используются различные методы: аналитические, графические, таблицы. Аналитические и графические методы применяются для простых уравнений, например, для уравнения: 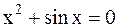 . Для более сложных уравнений строятся таблицы и определяются значения xi и xl+I, при которых функция y=f(x) меняет знак (поиск простых корней), или производные меняют знак (поиск кратных корней). Отсюда сразу можно сделать вывод, что задача нахождения простых корней существенно проще, чем задача отыскания кратных корней.
. Для более сложных уравнений строятся таблицы и определяются значения xi и xl+I, при которых функция y=f(x) меняет знак (поиск простых корней), или производные меняют знак (поиск кратных корней). Отсюда сразу можно сделать вывод, что задача нахождения простых корней существенно проще, чем задача отыскания кратных корней.
На этапе итерационного уточнения корней по одному и тому же алгоритму вычисляется последовательность значений x0, x1,..., 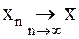 , при этом для вычисления последующих значений используются предыдущие значения. Поэтому для вычисления значения x1 задается значение x0, которое называется начальным приближением. Соответственно значение x1 называется первым приближением и т.д.
, при этом для вычисления последующих значений используются предыдущие значения. Поэтому для вычисления значения x1 задается значение x0, которое называется начальным приближением. Соответственно значение x1 называется первым приближением и т.д.
В основе алгоритма лежит итерационная формула (название происходит от латинского слова “iteracio”-повторение). Для нахождения корня с точностью e используется та или иная итерационная формула. Итерационный метод называется одношаговым, если для вычисления очередного приближения xn используется только xn-1 приближение, и k–шаговым, если используются k предыдущих приближений: xn-1,xn-2,...,xn-k.
Критерий сходимости. Для сходимости итерационного процесса необходимо и достаточно выполнение следующего условия:
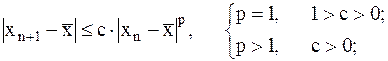 (6.1)
(6.1)
где c и p - некоторые константы, число p называется порядком сходимости метода.
При p=1 и с<1, метод обладает линейной сходимостью. Если p>1, то имеем сверхлинейную сходимость, если p=2, то имеем квадратичную сходимость. Если для всех n выполняется условие:  , где q<1, то говорят о сходимости со скоростью геометрической прогрессии.
, где q<1, то говорят о сходимости со скоростью геометрической прогрессии.
Критерий окончания. Точное значение корня мы не знаем. Когда же закончить итерационный процесс, чтобы утверждать, что 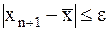 ?
?
Для каждого итерационного процесса существует свой критерий окончания в виде неравенства: 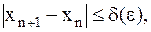 где d(e)-функция от e, при выполнение которого всегда имеет место неравенство:
где d(e)-функция от e, при выполнение которого всегда имеет место неравенство: 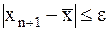 .
.
§2. Метод Ньютона (метод касательных). Пусть корень локализован на отрезке [a,b]. Выбирается точка x0 на этом отрезке и в этой точке строится касательная к графику функции y=f(x). За новое приближение x1 принимается точка, в которой касательная пересекает ось 0x. Далее процесс повторяется. Таким образом, на каждом этапе решение исходного уравнения заменяется на решение линейного уравнения (уравнения касательной), т.е. проводится линеаризация исходного уравнения.
Запишем уравнение касательной в точке xn:
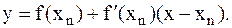 (6.2)
(6.2)
Полагая в, что при x=xn+1 имеем y=0 получаем формулу метода Ньютона:
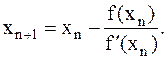 (6.3)
(6.3)
Критерий окончания метода Ньютона:
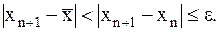 (6.4)
(6.4)
§3. Метод Ньютона для системы нелинейных уравнений. Пусть имеется следующая система нелинейных уравнений:
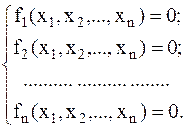 (6.5)
(6.5)
Как уже отмечалось выше, для одной переменной метод Ньютона использует замену искомого уравнения уравнением прямой или, как еще говорят, производит линеаризацию исходного уравнения. Пусть имеется k - ое приближение: 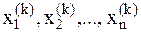 . Разложим левые части системы уравнений в ряд Тейлора и учтем только линейные члены:
. Разложим левые части системы уравнений в ряд Тейлора и учтем только линейные члены:
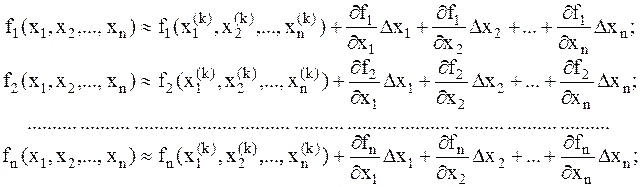 (6.6)
(6.6)
где 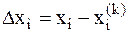 , i=1,2,...,n; а частные производные вычисляются в точке k-го приближения: x1=x1(k), x2=x2(k),...,xn=xn(k).
, i=1,2,...,n; а частные производные вычисляются в точке k-го приближения: x1=x1(k), x2=x2(k),...,xn=xn(k).
Заменим в исходной системе нелинейные функции fi(x1,x2,...,xn) на правые части этих приближенных равенств, которые являются линейными функциями относительно переменных Dxi, i=1,2,...,n. В итоге получим следующую систему линейных уравнений относительно переменных Dxi, i=1,2,...,n:
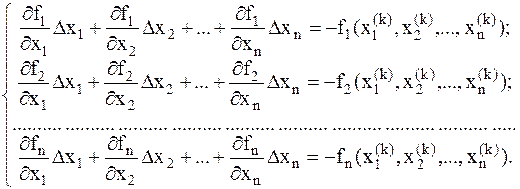 (6.7)
(6.7)
Из этой системы можно определить значения Dxi, i=1,2,...,n и вычислить значения k+1-приближения: 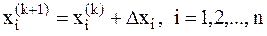 . Данная система уравнений представляют собой метод Ньютона для системы нелинейных уравнений.
. Данная система уравнений представляют собой метод Ньютона для системы нелинейных уравнений.
Определитель этой системы называется якобианом.
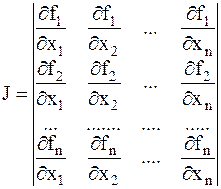 . (6.8)
. (6.8)
Для существования решения якобиан должен быть отличен от нуля для каждого шага итерации.
Критерий окончания. Итерационный процесс продолжается до тех пор, пока не выполнятся условия: 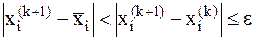 , для всех i=1,2,...,n.
, для всех i=1,2,...,n.
Варианты задания №9
С помощью метода Ньютона решить следующую систему уравнений, результаты получить с точностью 0,1.
1. 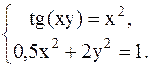 2.
2. 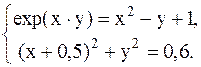
3. 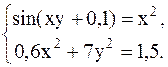 4.
4. 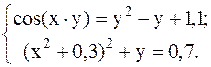
5. 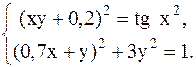 6.
6. 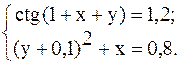
7. 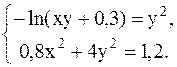 8.
8. 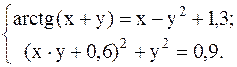
9. 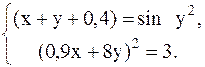 10.
10. 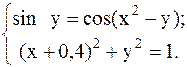
11. 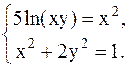 12.
12. 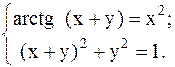
13. 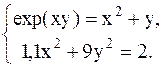 14.
14. 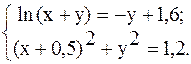
15. 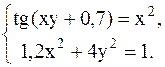 16.
16. 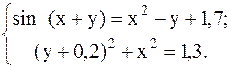
17. 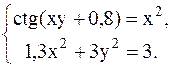 18.
18. 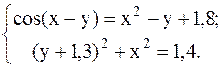
19. 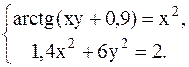 20.
20. 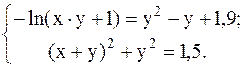
21. 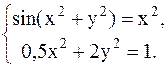 22.
22. 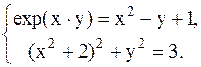
23. 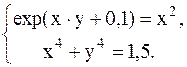 24.
24. 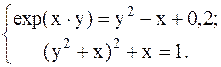
25. 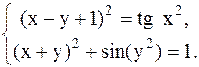 26.
26. 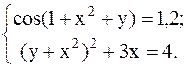
27. 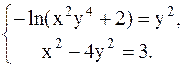 28.
28. 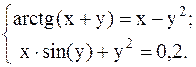
29. 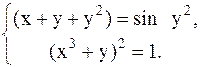 30.
30. 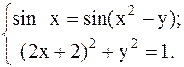
31. 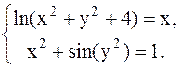 32.
32. 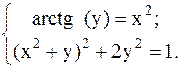
33. 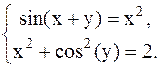 34.
34. 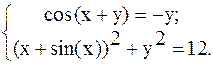
35. 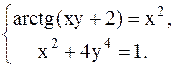 36.
36. 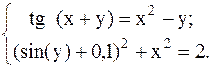
37. 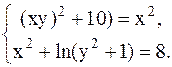 38.
38. 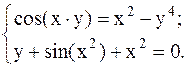
39. 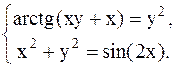 40.
40. 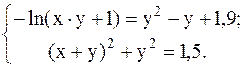
 2015-03-22
2015-03-22 1298
1298
