Вычислим изображение единичной функции и экспоненты
Пр.1  ( t ) =
( t ) = 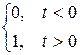 ,
,  ( t ) =:
( t ) =: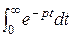 =
= 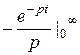 =
= 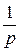 ,
,
Re p > 0
Пр.2 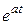 =
= 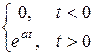 ,
, 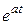 =:
=: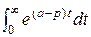 =
= 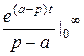 =
= 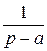 ,
,
Re p > a = s 0
Свойство линейности. Т.к. интеграл от суммы функций равен сумме интегра-лов, то линейной комбинации оригиналов соответствует линейная комбина-ция изображений.
С 1 f 1(t) + С 2 f 2(t) =: С 1 F 1(p) + С 2 F 2(p)
Из формулы Эйлера eit = cos t + i sin t имеем соs t = ½(eit + e-it), sin t = ½ i (eit - e-it) и для оригиналов этих функций вычислим изображения
Пр.3 f (t) = cos t = ½(eit + e-it) =: ½ [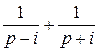 ] =
] = 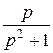
Пр.4 f (t) = sin t = ½ i (eit - e-it) =: 1/2 i [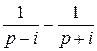 ] =
] = 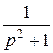
Пр.5 f (t) = t =: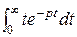 =
=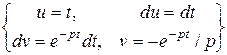 =
=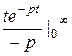 +
+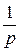
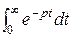 = =
= = 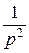 . f (t) = t 2 =:
. f (t) = t 2 =: 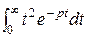 =
= 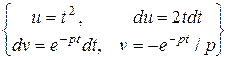 =
= 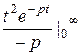 + +
+ +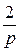
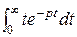 =
=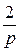
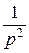 =
= 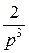 . Аналогично имеем t 3 =:
. Аналогично имеем t 3 =: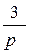
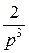 , t 4 =:
, t 4 =: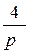
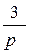
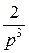 ,... и получаем tn =:
,... и получаем tn =: 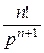 .
.
 2014-01-24
2014-01-24 868
868








