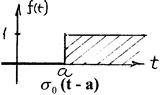
Пр.9 По данному графику оригинала найти изображение.
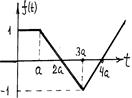
Построим аналитическое выражение для данной функции,
на основе общего уравнения прямой, проходящей через
две точки (t 1, y 1), (t 2, y 2) 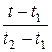 =
= 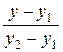 (5)
(5)
 и свойств единичной функции
и свойств единичной функции  (t - а) =
(t - а) = 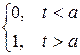
 (t)
(t)  (t) -
(t) -  (t - а)
(t - а)
Решение. Функцию на интервале [0, a] описывает разность двух единичных функций  (t) -
(t) -  (t - а). Первую наклонную определим из (5) по точкам (2 а, 0), (а, 1): y =-
(t - а). Первую наклонную определим из (5) по точкам (2 а, 0), (а, 1): y =-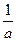 (t – 2 a). Для перехода от бесконечной прямой к отрезку на интервале [ a, 3 a ] умножим уравнение на разность
(t – 2 a). Для перехода от бесконечной прямой к отрезку на интервале [ a, 3 a ] умножим уравнение на разность (t -а) -
(t -а) - (t -3 а) Вторую наклонную определим из (5) по точкам (4 а,0), (3 а,-1): y =
(t -3 а) Вторую наклонную определим из (5) по точкам (4 а,0), (3 а,-1): y =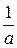 (t – 4 a), и умножим уравнение на
(t – 4 a), и умножим уравнение на  (t - 3 а). Сумма этих трех выражений определит аналитический вид функции
(t - 3 а). Сумма этих трех выражений определит аналитический вид функции
f (t) =  (t) -
(t) -  (t - а) -
(t - а) - 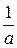 (t – 2 a) [
(t – 2 a) [ (t - а) -
(t - а) -  (t - 3 а)] +
(t - 3 а)] + 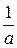 (t – 4 a) [
(t – 4 a) [ (t - 3 а)]
(t - 3 а)]
Представим f (t) в виде суммы слагаемых двух типов  (t - b) и (t – b)
(t - b) и (t – b) (t - b)
(t - b)
f (t) = (t) -
(t) - (t - а) -
(t - а) -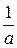 (t – a)
(t – a) (t - а) +
(t - а) + (t - а) +
(t - а) +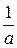 (t – 3 a)
(t – 3 a) (t - 3 а) +
(t - 3 а) + (t - 3 а)+
(t - 3 а)+
+ 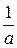 (t – 3 a)
(t – 3 a)  (t - 3 а) -
(t - 3 а) -  (t - 3 а) =
(t - 3 а) =  (t) -
(t) - 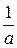 (t – a)
(t – a) (t - а) +
(t - а) + 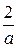 (t – 3 a)
(t – 3 a) (t - 3 а)
(t - 3 а)
С помощью соотношений Пр.8 совершим переход к искомому изображению
F (t) =: 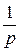 -
- 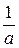
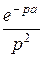 +
+ 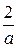
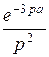 .
.
 2014-01-24
2014-01-24 2194
2194








