Таблица изображений
| № | f (t) при t >0 | F (p) | № | f (t) при t>0 | F (p) |
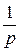
| t cos at | 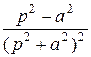
| |||
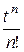
| 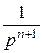
| t sin at | 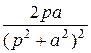
| ||
| eat | 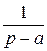
| 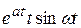
| 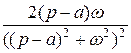
| ||
| cos at | 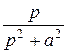
| 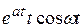
| 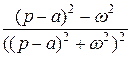
| ||
| sin at | 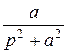
| 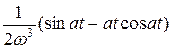
| 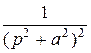
| ||
| ezt cos at | 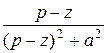
| 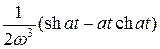
| 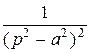
| ||
| ezt sin at | 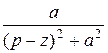
| 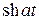
| 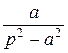
| ||
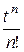 eat eat
| 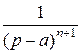
| 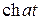
| 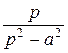
|
Если изображение является дробно-рациональной функцией F (p) = 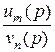 и m < n,то многочлен знаменателя представим в виде произ-ведения линейных множителей
и m < n,то многочлен знаменателя представим в виде произ-ведения линейных множителей 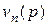 =
= 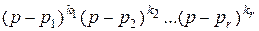 . Корни многочлена pi могут быть действительными числами, комплексными числами и кратными. Комплексные корни входят сопряженными парами и приводят к трехчленам типа (p 2 +
. Корни многочлена pi могут быть действительными числами, комплексными числами и кратными. Комплексные корни входят сопряженными парами и приводят к трехчленам типа (p 2 + 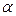 p +
p + 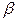 ). В результате F (p) представ-ляется в виде суммы элементарных дробей типа
). В результате F (p) представ-ляется в виде суммы элементарных дробей типа 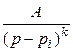 ,
, 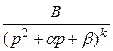 (метод неопределенных коэффициентов). Комбинируя эти дроби, можно пытаться построить изображения основных элементарных функций и затем по таблице восстановить оригинал.
(метод неопределенных коэффициентов). Комбинируя эти дроби, можно пытаться построить изображения основных элементарных функций и затем по таблице восстановить оригинал.
Пр. 10 Найти оригинал функции F (p) = 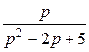 .
.
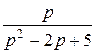 =
= 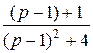 =
= 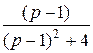 + ½
+ ½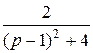 =: et cos 2 t + ½ et sin 2 t
=: et cos 2 t + ½ et sin 2 t
Пр. 11 Найти оригинал функции F (p) = 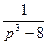 .
.
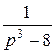 =
= 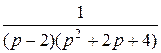 =
= 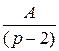 +
+ 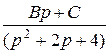 = =
= =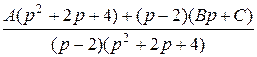
p2 | A + B = 0
p1 | 2A – 2B + C = 0 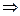 A = 1/12, B = -1/12, C = - 1/3
A = 1/12, B = -1/12, C = - 1/3
p0 | 4A – 2C = 1
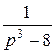 =
= 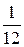
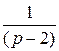 -
- 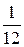
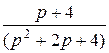 =
= 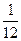
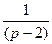 -
- 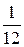
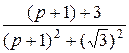
Из формул № 3, 6, 7 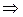 оригинал f (t) =
оригинал f (t) =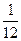 e 2 t -
e 2 t - 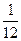 e-t (cos t
e-t (cos t 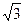 +
+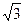 sin t
sin t 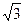 ).
).
Если в F (p) только простые нули: 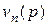 =
= 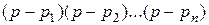 , то разложение изображения упрощается
, то разложение изображения упрощается
F (p) = 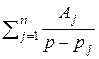 , где
, где 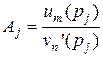 (6)
(6)
Пр.12 Найти оригинал функции F (p) = 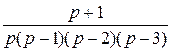
Вычисляем производную от знаменателя 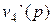 = [ p (p – 1)(p – 2)(p – 3) ]` =
= [ p (p – 1)(p – 2)(p – 3) ]` =
= (p – 1)(p – 2)(p – 3) + p (p – 2)(p – 3) + p (p – 1)(p – 3) + p (p – 1)(p – 2),
находим её значения в нулевых точках v 4`(0) = - 6, v 4`(1) = 2, v 4`(2) = - 2, v 4`(3) = 6, определяем коэффициенты A 0 = - 1/6, A 1 = 1, A 2 = - 3/2, A 3 = 2/3
и по формуле (6) расписываем разложение изображения на простые дроби
F (p) = 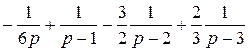 =:
=: 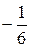 +
+ 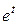 -
- 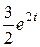 +
+ 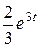 .
.
Если F (p) разлагается в сходящийся ряд
F (p) = 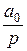 +
+ 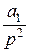 +
+ 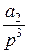 +... +
+... + 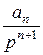 +...,
+...,
то его оригинал находится по формуле
f (t) = 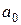 +
+ 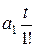 +
+ 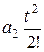 +... +
+... + 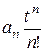 +...
+...
Этот ряд сходится при всех значениях t.
Пр.13 Найти оригинал функции F (p) = 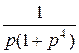 .
.
Используем формулу для суммы бесконечной геометрической прогрессии
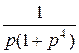 =
=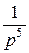
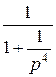 =
= 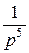 -
- 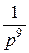 +
+ 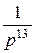 -... Этот ряд сходится при | p | > 1
-... Этот ряд сходится при | p | > 1
По формуле № 2 получаем оригинал f (t) = 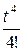 -
- 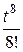 +
+ 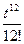 -
- 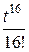 +...
+...
 2014-01-24
2014-01-24 934
934








